The Tully-Fisher relation (TFR) is an empirical correlation between luminosities and rotation velocities of disk galaxies. Since rotation velocity can be measured independent of distance, this correlation allows astronomers to use disk galaxies as standardizable candles for distance measurements. Once the correlation is calibrated using distances from Cepheid variables in nearby galaxies, the TFR extends the distance ladder beyond 100 Mpc, allowing measurements of the Hubble constant relatively unaffected by local gravitational motions deviating from the cosmic expansion (i.e., peculiar velocities). Establishing a precise and unbiased TFR is thus of paramount importance to observational cosmology.
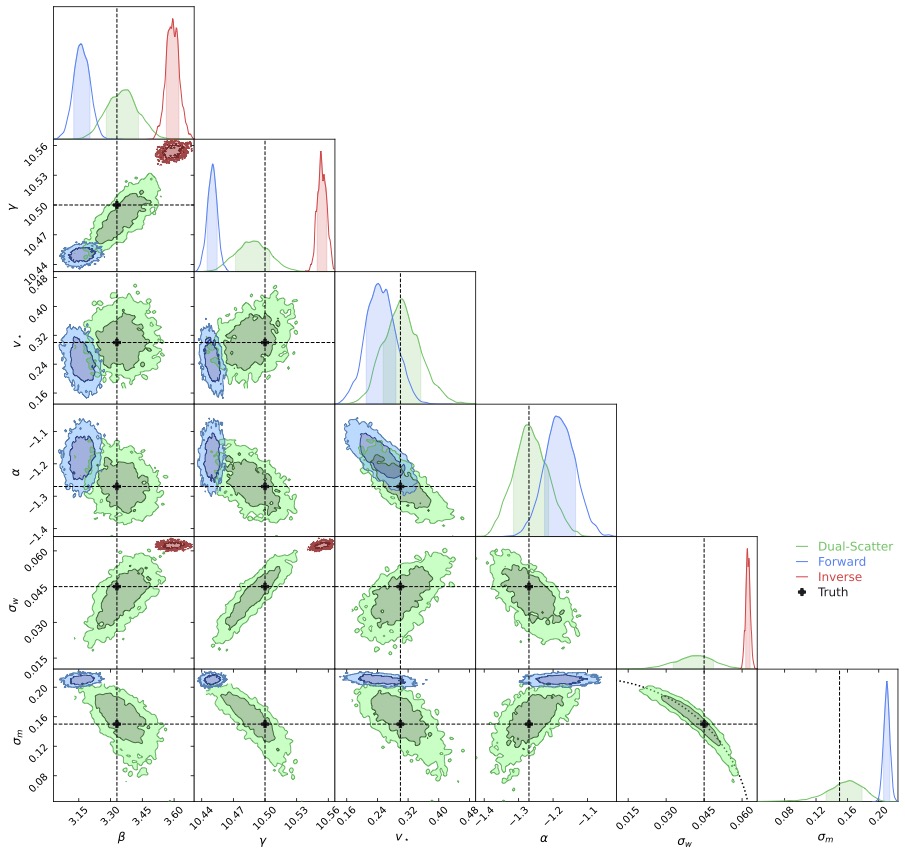
Above: MCMC-sampled posterior pdfs from the dual-scatter model (green) compared to those from the forward model (blue) and the inverse model (red). The input parameters are indicated by black dashed lines and black crosses. The dual-scatter model produces relatively unbiased inferences for all parameters, gives realistic statistical uncertainties, and reveals parameter degeneracies.
Although the TFR is often described as a linear correlation in logarithmic scales, the inference of its slope and intercept is not a simple linear regression problem, because of several important differences:
- The dependent variable (luminosity or mass) is a combination of two observables - the apparent magnitude and the luminosity distance from redshift.
- The independent variable (maximum rotation velocity) requires deprojecting the apparent HI line width to the edge-on perspective. So it requires estimating the inclination angle of the disk relative to the line-of-sight.
- There are measurement errors involved in all four observables, and there are intrinsic scatters in both axes.
Because of these characteristics, precise and unbiased inference of the TFR is hindered by one major source of measurement error (inclination angle) and two major statistical biases:
- The Distance-Dependent Malmquist Bias in Luminosity due to (1) the separation of magnitude limit and luminosity limit in a sample covering a range of distances, and (2) the measurement errors and the intrinsic scatter in luminosity.
- The Generalized Eddington Bias in Luminosity due to (1) non-uniform distributions of galaxies in rotation velocity, and (2) the measurement errors and the intrinsic scatter in rotation velocity.
These problems are not readily handled by previous methods such as the Gaussian-mixture dual-scatter method by Kelly (2007) and the maximum likelihood method of Willick (1994) and Willick et al. (1997). Both methods require the line widths to be individually corrected by the uncertain inclination angle, so low-inclination galaxies (i < 45 deg) must be excluded to avoid the most problematic corrections. In addition, the former cannot mitigate the distance-dependent Malmquist bias because distance is not separated from magnitude, and the latter cannot mitigate the generalized Eddington bias because it ignores the measurement error and the scatter of the independent variable.
In Fu (2025), I discussed the forementioned issues and provided solutions to mitigate these problems:
- To avoid errors associated with inclination measurements, galaxy inclination is treated as a latent variable with a known probability distribution function (pdf) and this pdf is marginalized when computing the data likelihood function.
- To mitigate the Malmquist bias, magnitudes and redshift-inferred distances are kept separate in all expressions, and the conditional probability of magnitude is re-normalized by its integral from the luminosity limit to account for the distance-dependent sample incompleteness.
- To mitigate the Eddington bias, two approaches are provided: (1) an analytical formula of the bias is derived and implemented to correct the bias in the data in an iterative fashion, (2) both the Schechter distribution function and the error and scatter of the independent variable are included in the data likelihood function of a model coined bidirectional dual-scatter model. The model is bidirectional because equivalent likelihood functions are derived regardless whether rotation velocity or luminosity is chosen as the independent variable.
The precision and efficacy of the likelihood-based method in mitigating the biases is thoroughly tested with synthetic data sets that realistically simulate (1) the Schechter luminosity function of galaxies, (2) the distribution in inclination angle and redshift, (3) the data censorship due to detection limit, and (4) the measurement errors and intrinsic scatters in both luminosity and rotation velocity. The methods presented in this work have the potential to facilitate precise, unbiased estimates of the Hubble constant through disk galaxies beyond 100 Mpc.
For more details, please refer to the ApJ paper and the GitHub repository.