Scientific Computing Using Python - PHYS:4905 - Fall 2018

Lecture #21 - 11/13/2018 - Prof. Kaaret

Homework #15 is at the bottom of this page.

Squaring the circle

Numerical integration is the use of an algorithm to calculate the value of a definite integral.  It is also refereed to as quadrature, which is a historical mathematical term that means calculating area of a geometric shape by constructing a square with the same area.  The "quad" is the same root that leads us to use the name quadratic for a polynomial in which the highest power is a square.  People have been working on quadrature since Babylonian times.  There is a papyrus from Egypt from around 1550 BC that states that "a circle's area stands to that of its circumscribing square in the ratio 64/81".  If you  think about this, it means that the Egyptians knew the value of π to an accuracy of 0.6%.


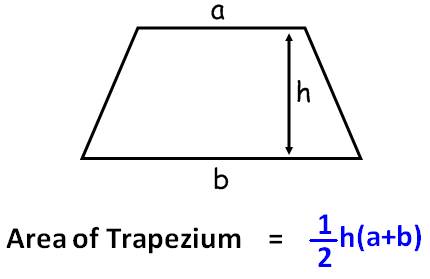
Trapezium

We will consider the problem of finding an approximate numerical value of the integral of a function f(x), the integrand, over an interval [a, b],

I=∫abf(x)dxI = \underoverset{a}{b}{∫} f(x) \, dx
We evaluate the function at n+1 points equally distributed in [a, b].  The spacing between adjacent points is then Δx = (b-a)/n.  and the x-values are xk = a +k Δx, where k = 0, 1, ..., n. 

A simple algorithm would be approximate each interval by a rectangle with a width of Δx and a height equal to value of the function at the left edge.  This is called a left Riemann sum.  As you can see from the figure below.  The left Riemann sum is not a great way to calculate an integral.  It works if you make your bins fine enough (at the cost of more computations), but it underestimates the integral in regions where the function slope is positive and overestimates it where the slope is negative.  One could instead use a right Riemann sum, taking the function value at the right edge, but it has the same issues, only reversed.




A better thing to do is to use a trapeze.  Oops, that's for the circus.  I meant a trapezium.  The Trapezium is a tight open cluster of stars in the heart of the Orion Nebula, named for its four brightest stars.



Trapezium is also the word used in English outside North America to denote a convex quadrilateral with at least one pair of parallel sides.  Most of us in this class call such an object a trapezoid.

Trapezoids offer a more accurate way to estimate an integral.  The idea is that rather than draw a rectangle with a height set by the function value at one edge, let's draw a trapezoid between the two edges.  For reasonably smooth functions, this often provides a nice approximation to the function, and therefore a more accurate estimate of its integral.

See the source image



The area of a trapezoid is (a+b)h/2, where h is its height and a and b are the lengths of the two sides.

See the source image

We'll flip the trapezoid on its side, so that h→Δx,a→f(xk),b→f(xk+1)h → Δx, \; a → f(x_k), \; b → f(x_{k+1}) .  The area of each trapezoid is then Ak=Δx[f(xk)+f(xk+1)]/2A_k = Δx \, \left[ f(x_{k}) + f(x_{k+1}) \right]/2. 

To calculate the integral, we sum the areas of all of the trapezoids.  For the first trapezoid, we'll have

A1=Δx[f(x0)2+f(x1)2]A_1 = Δx \, \left[ \frac{f(x_0)}{2} + \frac{f(x_1)}{2} \right]
When we add in the second one we get

A1+A2=Δx[f(x0)2+f(x1)2+f(x1)2+f(x2)2]=Δx[f(x0)2+f(x1)+f(x2)2]A_1 + A_2 = Δx \, \left[ \frac{f(x_0)}{2} + \frac{f(x_1)}{2} + \frac{f(x_1)}{2} + \frac{f(x_2)}{2} \right] = Δx \, \left[ \frac{f(x_0)}{2} + f(x_1) + \frac{f(x_2)}{2} \right]
Adding the third,

A1+A2+A3=Δx[f(x0)2+f(x1)+f(x2)+f(x3)2]A_1 + A_2 + A_3 = Δx \, \left[ \frac{f(x_0)}{2} + f(x_1) + f(x_2) + \frac{f(x_3)}{2} \right]

Note that we have to pay special attention to the first and last points because they only contribute to one trapezoid while all of the other points contribute to two.

Our approximation for the integral is then

∫abf(x)dx≈Δx[f(x0)2+f(x1)+⋯f(xn-1)+f(xn)2]\underoverset{a}{b}{∫} f(x) dx ≈ Δx \, \left[ \frac{f(x_0)}{2} + f(x_1) + ⋯ f(x_{n-1}) + \frac{f(x_n)}{2} \right]
Doing numerical integration this way is called using the trapezoid rule and this formula is called the extended trapezoid rule. 

We can write a Python function to do numerical integration via the trapezoid rule using the following steps.
  1. Take as input, the name of the function to be integrated (f), the endpoints of the interval of integration (a, b), and the number of points to use (n).
  2. Create an array with xk values evenly spaced from a to b.
  3. Evaluate the function at each xk value.
  4. Evaluate the sum in the equation above.
  5. Return the sum multiplied by the spacing between the points as an estimate of the integral.


Thomas Simpson's rule

Approximating our function with trapezoids is nice, but it misses sometimes, particularly if there is a maximum or minimum between our x-values or the function has curvature.  The trapezoid rule approximates the integrand by drawing a line between adjacent pairs of points.  Instead, we could take adjacent triples of points, draw a parabola through those three points, and integrate that parabola analytically.  This often does a better job as nicely shown the figure below (drawn by Popletibus),





The formula for the area for one interval is

∫x1x3f(x)dx≈Δx3[f0+4f1+f2]\underoverset{x_1}{x_3}{∫} f(x) dx \; ≈ \; \frac{Δx}{3} \left[f_0 + 4 f_1 + f_2 \right]
Note that if you substitute x0 = donut, x2 = beer, f(x)= Homer(x), you can re-write this as Homer Simpson's rule,

See the source image



To calculate the integral, we sum the integrals of all our little parabolas.  Note that we move by 2Δx each time so that successive integration intervals don't overlap.  The extended Simpson's rule for calculating an integral is

∫abf(x)dx≈Δx3[f(x0)+4f(x1)+2f(f2)+4f(x3)+⋯+2f(xn-1)+4f(xn-1)+f(xn)]\underoverset{a}{b}{∫} f(x) dx ≈ \frac{Δx}{3} \, \left[ f(x_0) + 4 f(x_1) + 2 f(f_2) + 4 f(x_3) + ⋯ + 2 f(x_{n-1}) + 4 f(x_{n-1}) + f(x_n) \right]
The coefficients alternate between 4 and 2 all the way through the middle of the sum.  Note that n needs to be an even number so that we have an odd number of terms in the sum.

The algorithm for doing integration via Simpson's rule is very similar to that for the trapezoidal rule, but the sum is different.


Higher power?

You might ask, why stop at quadratic polynomials?  There is a Simpson's rule that uses cubic polynomials and the so-called Newton–Cotes formulae allow any degree of polynomial.  However, one reaches diminishing returns because high order polynomials tend to oscillate around the points they are drawn through and don't actually provide better approximations.  This is especially true if the function has jumps, as seen in the figure below that shows approximations to a step function with polynomials of 3rd, 5th, and 7th order and with the trapezoid rule.  The trapezoid rule clearly does a better job.




In general, numerical integration methods tend to work well for smooth functions and poorly for functions with sharp features or oscillations over scales close to the integration step size (Δx in our discussions above).  If your function has one or a few discrete steps at known locations, then it is better to break the integration up into pieces with edges at the step locations.  If your function oscillates, then  you need to have at least several integration bins within each oscillation period.


Adapt  or perish

The accuracy of our estimation of the integral using either the trapezoid rule or Simpson's rule is essentially set by the number of grid points.  More points means a smaller step size leading to a better approximation of the function.  The method don't include a means to estimate the accuracy of the integration because that depends on how well they approximate the function, which is impossible to know precisely unless one can evaluate the integral analytically, in which case one should do that rather than doing a whole bunch of computations, or one evaluates the function at all points in the integration interval, which would take an infinite amount of time.

Usually, one estimates the accuracy by comparing the numerical estimates obtained with different grid spacing.  E.g. find the integral using 1000 grid points, do it again with 2000 grid points, and then take the absolute value of the difference as an estimate of the accuracy.  If the integrand is relatively smooth, so higher order derivatives are not too large, then the accuracy of the trapezoid rule scales with (Δx)3(Δx)^3 while the accuracy of Simpson's rule scales with (Δx)5(Δx)^5.  You will check this in the homework assignment below.

In adaptive quadrature, the algorithm adjusts the grid to obtain the desired accuracy.  In simplest adaptive quadrature algorithm, one
  1. Chooses an grid size and applies a method like the trapezoid rule or Simpson's rule to estimate the integral.  We'll call the value of the integral I0.
  2. Divides the step size in half and repeats the numerical integration. We'll call the new value of the integral I1.
  3. Checks if the desired accuracy has been reaches, specifically check if abs(I1 - I0) < itol*abs(I1), where itol is the desired fractional accuracy.  If we have reached the desired accuracy, then we are done and we return I1.  If not, we set I0 = I1  and go back to step 2.
Such algorithms are called "globally" adaptive because they adjust the whole grid.  The trapezoidal rule and Simpson's rule are particularly useful because we get to re-use all of the function evaluations as we make the grid finer by dividing the step size in half.  The trapezoidal rule is particularly computationally efficient because we don't even have to redo the sum over those points.

I0=∫abf(x)dx≈Δx[f(a)2+f(a+Δx)+⋯f(a+(n-1)Δx)+f(b)2]I_0 = \underoverset{a}{b}{∫} f(x) dx ≈ Δx \, \left[ \frac{f(a)}{2} + f(a+Δx) + ⋯ f(a + (n-1)Δx) + \frac{f(b)}{2} \right]
becomes

I1=∫abf(x)dx≈Δx2[f(a)2+f(a+Δx/2)+f(a+Δx)+f(a+3Δx/2)+⋯+f(b)2]I_1 = \underoverset{a}{b}{∫} f(x) dx ≈ \frac{Δx}{2} \, \left[ \frac{f(a)}{2} + f(a+Δx/2) + f(a+Δx) + f(a+3Δx/2) + ⋯ + \frac{f(b)}{2} \right]
=I02+Δx2[f(a+Δx/2)+f(a+3Δx/2)+⋯]= \frac{I_0}{2} + \frac{Δx}{2} \left[ f(a+Δx/2) + f(a+3Δx/2) + ⋯ \right]
We can simply add the old sum to the new sum with the new points.  We don't even have to keep the values from the function evaluations on the coarser grid.

The disadvantage of globally adaptive quadrature is that the finer grid spacings can become computationally expensive.  In locally adaptive quadrature, one breaks the interval into pieces and refines the grid only for the pieces where the integral is not sufficiently accurate.  For example, one might
  1. Evaluate the integral in the intervals [a, (a+b)/2] and [(a+b)/2, b], i.e. divide the original interval in half, using a step size of Δx.
  2. Evaluate the integral in the same intervals using a step size of Δx/2.
  3. For each of those intervals, check if we have reached the desired accuracy using the same equation as in step 3 for global quadrature.  Note that if we achieve the desired fractional accuracy in all intervals, then we will achieve it globally.
  4. For any interval where we have reached the desired accuracy, stop and record the integral for that interval.  For any interval where we have not reached the desired accuracy, split that interval into two pieces by going back to step 1 with a and b set to the edges of that interval.
Some locally adaptive quadrature algorithms have an additional check and stop if the global accuracy of the integral is good enough, i.e. they add up the contributions from all of the pieces at each step and stop if estimate of the total integral changes by less than itol even if that accuracy hasn't been achieved for each individual piece.  This keeps the algorithm from throwing computational resources into small pieces of the interval that are poorly behaved, but don't make a large contribution to the total integral.

Locally adaptive quadrature is rather more complex to program than globally adaptive quadrature.  Most people don't even try, but instead use a software package called QUADPACK that was written in Fortran in the 1980s.  There is a 300 page book describing QUADPACK.  Fortunately, the SciPy library includes an interface to QUADPACK.  The routine scipy.integrate.quad uses locally adaptive quadrature to numerically integrate a function, f(x), in a given interval (a, b), to a specified relative accuracy epsrel, which is set by default to 1.49e-08.  It returns the value of the integral and an estimate of the error.  An example calling sequence is

from scipy.integrate import quad
integral, integral_err = quad(f, a, b)

The routine has many optional parameters and many more variables that it can return that are described at its reference page https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html.  There is also a version to do double integrals of functions with two variables, scipy.integrate.dblquad.


Homework #15

For HW #15, you will write Python code to perform numerical integration via the trapezoid rule and Simpson's rule and evaluate the accuracy of those routines.  Please hand in your code electronically.

Your code should have a function integrate_trapezoid that does numerical integration using the trapezoid rule and takes as input: the name of the function to be integrated (f), the endpoints of the interval of integration (a, b), and the number of points to use (n).  Write this function first and test it by integrating  f(x)=x2f(x) = x^2  over the interval [0, 10], which you should be able to check analytically.  Your code should have a similar function integrate_simpson that does numerical integration using Simpson's rule.

In the main body of your script, define the function

g(x) = (1+cos(x)) * exp(-x/(2*pi))

First plot this function over the interval x = [0, 60].

Then write a loop that integrates this function in the interval [0, 60] using different values for the number of points,  n=2j+1n = 2^j + 1 where j = 6, ... 16.  Do the integration using both the trapezoid rule and Simpson's rule.

For each n, plot the error in the numerical integration, which we will define as the absolute value of the difference between numerically calculated integral and the analytically calculated integral which is

4πe-30/π(-2π2+e30/π(1+2π2)-cos2(30∘)+πsin(60∘))1+4π2=6.4380153689449355472\frac{4π \, e^{-30/π} \left(-2 π^2 + e^{30/π} (1 + 2 π^2) - \cos^2(30^∘) + π \, \sin(60^∘) \right)} {1 + 4 π^2} = 6.4380153689449355472

versus the integration step size, Δx.  You should do this on a log-log scale.  Think about what trends you see.  In particular, does the error for each method depend on some power of Δx?  Include a comment block at the end of your code with some discussion of this.