Addendum 10: Gravitational time dilation (general relativity)

First define some astronomical and physics constants and dimensional units that may be needed below

1. Gravitational redshift: Pound-Rebka Experiment. Consider an experiment (cartoon below, at right) in which a laser is directed upward from the bottom tro the top of a lab in space which is unformly accelerating upward with acceleration a = -g. Assume at the instant the laser pulse starts, the lab is a rest (v=0).

When the laser pulse is received at the top, distance L from the bottom, the time is

However, at that time the speed of the observer at the top is now:

Therefore the observer will notice a redshift (since the observer is moving away from the source of light) caused by the Doppler effect:

Since the equivalence principle requires that all such experiements must also produce the same result in a stationary lab with the equivaent graviational acceleration, we must also see this effect in labs on Earth. This is called the gravitational redshift effect, and was first measured by Pound and Rebka at Harvard in 1960.

Example: the Pound-Rebka experiment consisted of observing a very narrow spectral of iron-57 (Fe⁵⁷). They place the source at the bottom of a stairway in the Physics Buyilding and the dtector at the top. The stairway was 74 feet high. The predicted fractional redshift was:

For more details on this experiment see: http://www.answers.com/topic/gravitational-redshift

2. Gravitational redshift: Full GR result, application to white dwarfs. The result above is an approximation useful for small L only, since we assumed the acceleration was constant form bottom to top of the lab. Using the full GR theory, the gravitational redshift can be shown to be:

Note: This expression reduces to the approximate form we had above if we expand using a Taylor series, using the approxmation r_s/r << 1. (Try it!)

Example: What are the expected fractional gravitational redshifts for spectral lines from the Sun and a typical white dwarf? (Assume both have 1 solar mass, and the wd has R~R_earth).

The GR redshift of a white dwarf is ~100x that of a normal star!

The gravitational redshift from the white dwarf Sirius-B was measured in 1924 and is one of three classic tests of General Relativity (although it is really a consequence of the equivalence principle, and is consistent with any theory of gravity that incorporates the equaivalence principle).

Example 2: The observed gravitational redshift of Sirius-B, converted to velocity, is V = 91 km/s and the mass is 1.05 Msun. Use these observations to determine the radius of Sirius-B

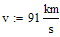
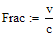
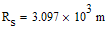
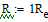
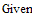
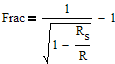
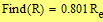
3. Gravitational time dilation. The gravitational redshift also implies time dilation: Clocks in gravitiational fields run more slowy than clocks in free space. The frequency of an atom's spectral lines are used as the fundamental time reference: This is how 'atomic' clocks work. (One second is defined as the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two of the energy levles of the Cesium133 atom.)

Recall that the wavelength of a spectral line of an atom is related to its frequency f by

Hence a fractional wavelength shift Dl/l corresponds to a frequency shift:

This means that time durations are different for observers in differing gravitational fields; the time duration Dt of an observer at distance R from a mass M relative to an observer far from any gravitational field is easily found from the expression for redshift:

Example: An astronaut orbits a 10 M_sun black hole at a radius of 35 km for 1 year (on her watch). She then returns to the parent spaceship, located very far from the black hole. How much time has elapsed at the spaceship? (Ignore the transit time to and from orbit)

Note: The astronaut, aproaching this close to the black hole, would experience unbearable tidal forces, as we previosuly calculated!