


Next: About this document ...
Introduction to Astrophysics II, 29:120
Spring, 2009
Steve Spangler's Whirlwind Guide to Synchrotron Radiation
Synchrotron radiation is electromagnetic radiation produced by relativistic electrons moving in a magnetic field. The following formulas are taken from the classic book Radio Astrophysics by A. Pacholczyk. These formulas use the cgs system of units.
Frequency at which emission occurs
Although synchrotron radiation can be produced by any charged particle, in astrophysics it is almost always electrons that are radiating. A single electron (or group of electrons with the same energy and pitch angle 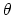 ) emit radiation in a range of frequencies around a characteristic frequency
) emit radiation in a range of frequencies around a characteristic frequency 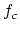 given by
given by
 |
(1) |
In equation (1) 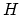 is the magnetic intensity in Oersteds. However, since in the cgs system of units the permeability of a vacuum is 1 (``saints be praised!''), one can also use the value of the magnetic induction in Gauss.
is the magnetic intensity in Oersteds. However, since in the cgs system of units the permeability of a vacuum is 1 (``saints be praised!''), one can also use the value of the magnetic induction in Gauss. 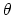 is the pitch angle of the particle (angle between the velocity and the direction of the magnetic field), and
is the pitch angle of the particle (angle between the velocity and the direction of the magnetic field), and 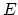 is the particle energy (ergs). The value of the constant
is the particle energy (ergs). The value of the constant
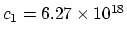 .
.
Note that the higher the energy of the particle, the higher the frequency at which it emits. Turning this around, observations of a source at a higher frequency are showing radiation from electrons of higher energy. X-ray synchrotron radiation is observed in some cosmic sources, and is an indication of extremely high energy electrons.
Radiation is emitted in a range of frequencies about 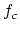 . The shape of the spectrum is given by the function
. The shape of the spectrum is given by the function
where 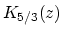 is a K-Bessel function of fractional order. The argument of the function
is a K-Bessel function of fractional order. The argument of the function 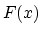 is the ratio of the frequency to the characteristic frequency,
is the ratio of the frequency to the characteristic frequency,
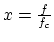 .
.
Spectrum of radiation from an ensemble of electrons
The incremental volume emissivity of synchrotron radiation from an incremental number of electrons 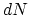 with energies in the range
with energies in the range
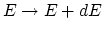 is
is
![\begin{displaymath}
d \epsilon (f) = dN \left[ \frac{\sqrt 3 e^3}{4 \pi m c^2} H \sin \theta F(x) \right]
\end{displaymath}](img15.png) |
(5) |
or
![\begin{displaymath}
d \epsilon (f) = dN \left[ c_3 H \sin \theta F(x) \right] \mbox{ with } c_3 = 1.87 \times 10^{-23}
\end{displaymath}](img16.png) |
(6) |
The energy dependence of this expression is contained in 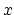 .
.
Energy loss due to synchrotron radiation
A particle radiating synchrotron radiation is losing energy at a rate
![\begin{displaymath}
\frac{dE}{dt} = - \left[ \frac{2e^4}{3m^4 c^7} \right] H^2 \sin^2\theta E^2 = c_2 H^2 \sin^2\theta E^2
\end{displaymath}](img18.png) |
(7) |
with
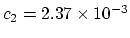 . Note that the higher the energy of the particle, the faster it loses energy.
. Note that the higher the energy of the particle, the faster it loses energy.
Radiation from a power law spectrum of electrons
Observations of Galactic cosmic ray electrons show that they have a power law spectrum of the form
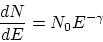 |
(8) |
so
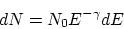 |
(9) |
If we substitute this into Equation (5) or (6) and integrate over energy, we find that (see details in Pacholczyk)
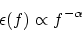 |
(10) |
with
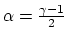 . A good graphical illustration of this integration and its result is given in Figure 28.5 of Carroll and Ostlie. This result is in good agreement with the overwhelmingly common observation of power law radio spectra, with a narrow dispersion in
. A good graphical illustration of this integration and its result is given in Figure 28.5 of Carroll and Ostlie. This result is in good agreement with the overwhelmingly common observation of power law radio spectra, with a narrow dispersion in 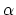 . The observed values of
. The observed values of 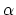 are close to that which characterizes the Galactic cosmic ray electrons.
are close to that which characterizes the Galactic cosmic ray electrons.



Next: About this document ...
Steve Spangler
2009-04-23
![]() ) emit radiation in a range of frequencies around a characteristic frequency
) emit radiation in a range of frequencies around a characteristic frequency ![]() given by
given by
![]() . The shape of the spectrum is given by the function
. The shape of the spectrum is given by the function

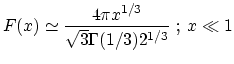
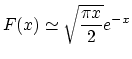
![\begin{displaymath}
d \epsilon (f) = dN \left[ \frac{\sqrt 3 e^3}{4 \pi m c^2} H \sin \theta F(x) \right]
\end{displaymath}](img15.png)
![\begin{displaymath}
\frac{dE}{dt} = - \left[ \frac{2e^4}{3m^4 c^7} \right] H^2 \sin^2\theta E^2 = c_2 H^2 \sin^2\theta E^2
\end{displaymath}](img18.png)