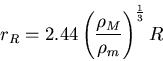Next: About this document ...
29:61 General Astronomy
Fall 2005
Constants and Formulas
Just the facts, Ma'am
Atmospheric Pressure
 Atmospheric pressure at sea level:
Atmospheric pressure at sea level:
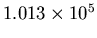 Newtons/m
Newtons/m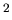
 Change in atmospheric pressure associated with increase in altitude
Change in atmospheric pressure associated with increase in altitude 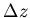
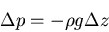 |
(1) |
where 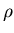 is the gas density (kilograms/m
is the gas density (kilograms/m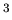 ),
), 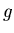 acceleration due to gravity at Earth's surface (9.8 m/sec
acceleration due to gravity at Earth's surface (9.8 m/sec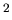 ).
).
 Perfect gas law
Perfect gas law
 |
|
|
(2) |
 |
|
|
(3) |
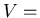 volume of gas,
volume of gas,  total number of particles (atoms and/or molecules) in the gas,
total number of particles (atoms and/or molecules) in the gas, 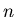 number density of atoms and/or molecules (units are particles/m
number density of atoms and/or molecules (units are particles/m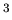 ),
),  is the temperature (degrees Kelvin),
is the temperature (degrees Kelvin),
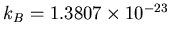 J/K.
J/K.
 Differential form of change in atmospheric pressure with altitude
Differential form of change in atmospheric pressure with altitude
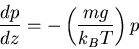 |
(4) |
where 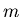 mass of atom or molecule composing the atmosphere.
mass of atom or molecule composing the atmosphere.
 Pressure as function of height in an isothermal atmosphere
Pressure as function of height in an isothermal atmosphere
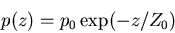 |
(5) |
 Isothermal pressure scale height
Isothermal pressure scale height
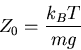 |
(6) |
The Orbit of the Moon and Eclipses
 The altitude angle of a celestial object at transit is
The altitude angle of a celestial object at transit is
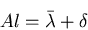 |
(7) |
where 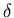 is the declination of the object, and
is the declination of the object, and 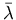 is the complement of the latitude.
is the complement of the latitude.
 The average inclination of the Moon's orbit to the plane of the ecliptic,
The average inclination of the Moon's orbit to the plane of the ecliptic,
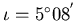 .
.
 The average angular diameter of the Sun as seen from Earth,
The average angular diameter of the Sun as seen from Earth,
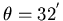 .
.
 The maximum distance
The maximum distance 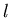 in back of an object in which an umbral eclipse of the Sun will be seen is
in back of an object in which an umbral eclipse of the Sun will be seen is
![\begin{displaymath}
l = \frac{d}{2\tan [\theta/2]}
\end{displaymath}](img26.png) |
(8) |
where 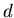 is the diameter of the object, and
is the diameter of the object, and 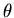 is the angular diameter of the Sun at that point (32 arcminutes at the orbit of the Earth).
is the angular diameter of the Sun at that point (32 arcminutes at the orbit of the Earth).
Eclipse Cycles and Precession
 Synodic period of the Moon:
Synodic period of the Moon:
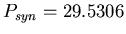 days.
days.
 Nodal period of the Moon:
Nodal period of the Moon:

 Condition for repetition of eclipses:
Condition for repetition of eclipses:
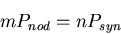 |
(9) |
with 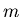 ,
,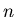 integers
integers
 Angular momentum of an object (with mass m) moving with velocity
Angular momentum of an object (with mass m) moving with velocity 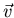 a distance
a distance  from the origin of a coordinate system:
from the origin of a coordinate system:
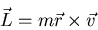 |
(10) |
 Definition of vector angular velocity
Definition of vector angular velocity 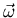 , such that
, such that
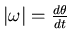 ,
,
 |
(11) |
Then,
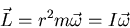 |
(12) |
With 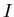 the moment of inertia.
the moment of inertia.
 Moment of inertia for uniform sphere of mass
Moment of inertia for uniform sphere of mass 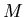 and radius
and radius 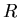 :
:
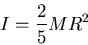 |
(13) |
 Definition of torque: causes change in angular momentum with time:
Definition of torque: causes change in angular momentum with time:
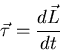 |
(14) |
Vector Cross Products, Newton's Laws, the Gravitational Force
 The definition of a vector cross product:
The magnitude of a cross product is defined as follows. If
The definition of a vector cross product:
The magnitude of a cross product is defined as follows. If
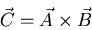 |
(15) |
then the direction of
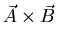 is given by the right hand rule.
The magnitude of
is given by the right hand rule.
The magnitude of
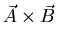 is given by
is given by
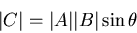 |
(16) |
where 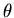 is the angle between the two vectors. Another way of expressing it as follows. Draw up an array
is the angle between the two vectors. Another way of expressing it as follows. Draw up an array
![\begin{displaymath}
\left[
\begin{array}{ccc}
\hat{e}_x & \hat{e}_y & \hat{e}_z \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{array}\right]
\end{displaymath}](img47.png) |
(17) |
For each component, knock out the column corresponding to that coordinate, and form the product of the remaining terms. The result for the vector is
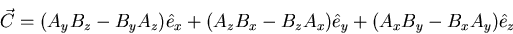 |
(18) |
 Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the
Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the 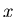 component of the vector, then the
component of the vector, then the 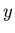 component, etc.
component, etc.
Newton's Laws of Motion
- An object in motion remains in motion with constant vector momentum
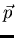 , unless acted upon by an external force. An object at rest has zero momentum, and therefore remains at rest.
, unless acted upon by an external force. An object at rest has zero momentum, and therefore remains at rest.
- If a force acts on an object, its momentum changes according to
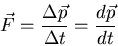 |
(19) |
If the mass of the object acted upon stays constant, this simplifies to
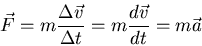 |
(20) |
where 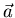 is the acceleration.
is the acceleration.
- If an object A exerts a force on B, B exerts a force on A which is equal in magnitude and opposite in direction to that exerted by A on B. Rather lyrically said, ``to every action there is an opposite and equal reaction''.
 Centripetal acceleration: If an object moves in a circle of radius
Centripetal acceleration: If an object moves in a circle of radius 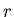 with speed
with speed 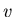 , it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
, it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
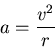 |
(21) |
 The gravitational force: If two objects possessing masses
The gravitational force: If two objects possessing masses 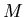 and
and 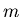 are a distance
are a distance 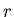 apart, there is an attractive force between them, the magnitude of which is
apart, there is an attractive force between them, the magnitude of which is
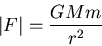 |
(22) |
where 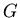 is the gravitational constant,
is the gravitational constant,
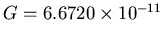 N-m
N-m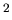 -kg
-kg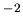 .
.
 The circular orbit equation. If
The circular orbit equation. If 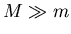 , and the orbit of
, and the orbit of 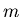 about
about 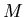 is circular, there is a relation between the radius of the orbit
is circular, there is a relation between the radius of the orbit 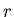 , the orbital speed
, the orbital speed 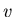 , and the mass
, and the mass 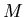 which is called the circular orbit equation. It says
which is called the circular orbit equation. It says
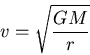 |
(23) |
Kepler's Laws, Radioactive Decay, Physics of Atmospheres
Orbits and Kepler's Laws
 Equations for an ellipse:
Equations for an ellipse:
In Cartesian coordinates:
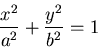 |
(24) |
where 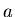 is the semimajor axis,
is the semimajor axis, 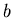 is the semiminor axis.
is the semiminor axis.
In polar coordinates 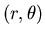 ,
,
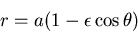 |
(25) |
where 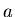 is the semimajor axis and
is the semimajor axis and 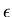 is the eccentricity of the ellipse.
is the eccentricity of the ellipse.
Eccentricity in terms of 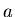 and
and 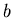 ,
,
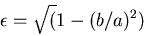 |
(26) |
 Kepler's 3rd Law:
Kepler's 3rd Law:
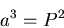 |
(27) |
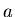 = semimajor axis of planetary orbit in astronomical units,
= semimajor axis of planetary orbit in astronomical units, 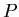 is the orbital period in years.
is the orbital period in years.
Radioisotope Dating
 Radioactive decay,
Radioactive decay,
 , where
, where  is the unstable parent isotope,
is the unstable parent isotope, 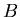 is the daughter isotope (product of the decay), and
is the daughter isotope (product of the decay), and 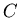 is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
 Exponential decay law:
Exponential decay law:
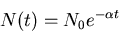 |
(28) |
where 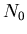 is the number of parent nuclei at
is the number of parent nuclei at  ,
, 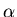 is the decay constant, and
is the decay constant, and 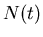 is the number of parent nuclei at time
is the number of parent nuclei at time 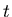 . The decay constant is related to the half life
. The decay constant is related to the half life  by
by
 |
(29) |
 Equation for determining age of formation of rock from ratio of isotopes.
Equation for determining age of formation of rock from ratio of isotopes.
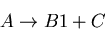 |
(30) |
where  is the radioactive parent isotope,
is the radioactive parent isotope, 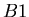 is the isotope of element
is the isotope of element 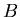 that is the daughter product of the decay reaction, and
that is the daughter product of the decay reaction, and 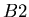 is the isotope of element
is the isotope of element 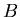 that is not the daughter product of the decay. Let
that is not the daughter product of the decay. Let 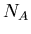 be the number of isotopes of
be the number of isotopes of  in a sample,
in a sample, 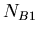 the number of isotopes of
the number of isotopes of 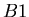 , and
, and 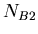 the number of isotopes of
the number of isotopes of 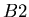 , then we have the following equation
, then we have the following equation
 |
(31) |
where 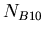 was the number of nuclei of isotope
was the number of nuclei of isotope 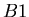 when the rock formed.
when the rock formed.
Physical Characteristics of the Planets
 Definition of density
Definition of density 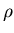
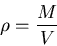 |
(32) |
where 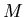 is mass and
is mass and 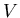 is volume. Units of density are kilograms/m
is volume. Units of density are kilograms/m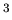 . Typical densities of common substances and astronomical objects are:
. Typical densities of common substances and astronomical objects are:
- water: 1000 kg/m
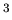
- rock: 2900 - 3900 kg/m
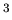
- aluminum: 2700 kg/m
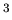
- brass: 8600 kg/m
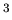
- lead: 11300 kg/m
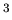
Physics of Planetary Atmospheres
 Escape speed from a planet
Escape speed from a planet
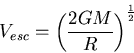 |
(33) |
where 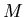 is the mass of the planet, and
is the mass of the planet, and 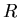 is its radius.
is its radius.
 root-mean-square (rms) molecular speed in a gas
root-mean-square (rms) molecular speed in a gas
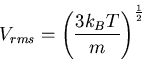 |
(34) |
where  is the temperature (K), and
is the temperature (K), and 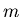 is mass of the molecule or atom in the gas.
is mass of the molecule or atom in the gas.
 Definition of the distribution function for molecular speeds
Definition of the distribution function for molecular speeds
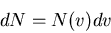 |
(35) |
is the differential number of molecules with speeds in the range
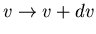 .
.
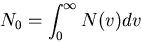 |
(36) |
where 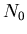 is the total number of molecules/m
is the total number of molecules/m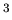 .
.
 The Maxwellian distribution function
The Maxwellian distribution function
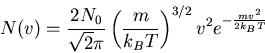 |
(37) |
This distribution describes the true distribution for gases in planetary atmospheres, as well as most other astronomical gases.
 Condition for retention of planetary atmosphere over geological timescales
Condition for retention of planetary atmosphere over geological timescales
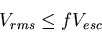 |
(38) |
where 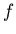 is a number between 1/6 and 1/4.
is a number between 1/6 and 1/4.
Planetary Magnetism
The Urey Cycle
 The mineralogical chemical cycle responsible for controlling the level of
carbon dioxide in the Earth's atmosphere.
The mineralogical chemical cycle responsible for controlling the level of
carbon dioxide in the Earth's atmosphere.
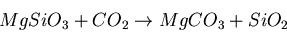 |
(39) |
The arrow can point to the right or the left, depending on the temperature.
Photoionization
 The ionization of molecules by ultraviolet light in the upper atmosphere of the Earth (and elsewhere).
The ionization of molecules by ultraviolet light in the upper atmosphere of the Earth (and elsewhere).
 |
(40) |
where 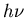 represents the energy present in a photon of light.
represents the energy present in a photon of light.
The Lorentz Force
 The force acting on a charged particle moving in electric
The force acting on a charged particle moving in electric  and magnetic
and magnetic 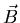 fields is given by .
fields is given by .
 |
(41) |
where 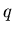 is the charge of the particle. For a proton, the charge is
is the charge of the particle. For a proton, the charge is
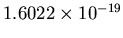 Coulombs, and for an electron,
Coulombs, and for an electron,
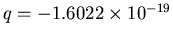 Often the symbol
Often the symbol 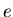 is used for this fundamental charge of an electron or proton. The units of magnetic field are Tesla, those of the electric field are Volts/meter.
is used for this fundamental charge of an electron or proton. The units of magnetic field are Tesla, those of the electric field are Volts/meter.
Electromagnetic Radiation
 Light corresponds to electromagnetic waves with wavelengths in the range
Light corresponds to electromagnetic waves with wavelengths in the range
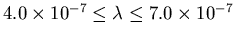 meters.
meters.
The Solar Constant
 The solar constant = 1370 W/m
The solar constant = 1370 W/m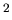 . For other planets, it is inversely proportional to the square of the distance from the Sun.
. For other planets, it is inversely proportional to the square of the distance from the Sun.
The Stefan Boltzmann Law
 A perfect blackbody radiator radiates the following amount of power into space per unit of surface area. The power consists of energy carried out by waves with a range of wavelengths.
A perfect blackbody radiator radiates the following amount of power into space per unit of surface area. The power consists of energy carried out by waves with a range of wavelengths.
 |
(42) |
where
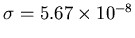 Watts/m
Watts/m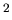 /K
/K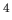 , and
, and  is the temperature in degrees Kelvin.
is the temperature in degrees Kelvin.
The Equilibrium Temperature of a Planet
 The equilibrium temperature of a planet, ignoring the greenhouse effect of its atmosphere (which often is a major correction) is
The equilibrium temperature of a planet, ignoring the greenhouse effect of its atmosphere (which often is a major correction) is
![\begin{displaymath}
T_{eq} = \left[ \frac{(1-A)S_0}{\sigma}\right]^{\frac{1}{4}}
\end{displaymath}](img117.png) |
(43) |
where 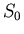 is the solar constant for that planet, and
is the solar constant for that planet, and  is the albedo.
is the albedo.
Wien's Law
 The wavelength at which a blackbody radiator is brightest,
The wavelength at which a blackbody radiator is brightest, 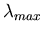 is given by
is given by
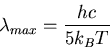 |
(44) |
where
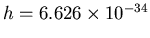 is Planck's constant,
is Planck's constant, 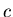 is the speed of light, and
is the speed of light, and  is the temperature.
is the temperature.
The Roche Limit
 The closest that a satellite can come to a planet (or small mass to a much larger mass) before it is torn apart by tidal stresses. This means that the tides (differential ``stretching'' force across the object becomes larger than the gravitational force holding the object together. The Roche limit is defined as a distance
The closest that a satellite can come to a planet (or small mass to a much larger mass) before it is torn apart by tidal stresses. This means that the tides (differential ``stretching'' force across the object becomes larger than the gravitational force holding the object together. The Roche limit is defined as a distance 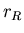 , such that
, such that
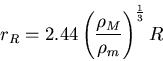 |
(45) |
where 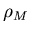 is the density of the massive object,
is the density of the massive object, 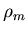 is the density of the smaller object (i.e. satellite), and
is the density of the smaller object (i.e. satellite), and 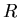 is the radius of the massive object.
is the radius of the massive object.
Resonant Perturbations
 A periodic perturbation is said to be resonant with a periodic system when
A periodic perturbation is said to be resonant with a periodic system when
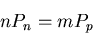 |
(46) |
where 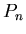 is the natural period of the unperturbed system (think of the orbital period of a satellite around a planet), and
is the natural period of the unperturbed system (think of the orbital period of a satellite around a planet), and 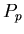 is the period of the periodic perturbing force (think of the orbital period of a satellite further out) and
is the period of the periodic perturbing force (think of the orbital period of a satellite further out) and 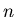 and
and 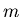 are any two integers. When equation (2) is satisfied, the perturbation produces a large change in the orbital properties of the object being acted on. For example, n=2, m=1 corresponds to the so-called 2:1 resonance, n=5, m=2 is the 5:2 resonance, etc. All of these can be seen in the form of ``holes'' in the rings of Saturn and Kirkwood's Gaps in the asteroid belt.
are any two integers. When equation (2) is satisfied, the perturbation produces a large change in the orbital properties of the object being acted on. For example, n=2, m=1 corresponds to the so-called 2:1 resonance, n=5, m=2 is the 5:2 resonance, etc. All of these can be seen in the form of ``holes'' in the rings of Saturn and Kirkwood's Gaps in the asteroid belt.



Next: About this document ...
Steve Spangler
2005-08-17
![]() Atmospheric pressure at sea level:
Atmospheric pressure at sea level:
![]() Newtons/m
Newtons/m![]()
![]() Change in atmospheric pressure associated with increase in altitude
Change in atmospheric pressure associated with increase in altitude ![]()
![]() Perfect gas law
Perfect gas law
![]() Differential form of change in atmospheric pressure with altitude
Differential form of change in atmospheric pressure with altitude
![]() Pressure as function of height in an isothermal atmosphere
Pressure as function of height in an isothermal atmosphere
![]() Isothermal pressure scale height
Isothermal pressure scale height
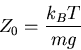
![]() The altitude angle of a celestial object at transit is
The altitude angle of a celestial object at transit is
![]() The average inclination of the Moon's orbit to the plane of the ecliptic,
The average inclination of the Moon's orbit to the plane of the ecliptic,
![]() .
.
![]() The average angular diameter of the Sun as seen from Earth,
The average angular diameter of the Sun as seen from Earth,
![]() .
.
![]() The maximum distance
The maximum distance ![]() in back of an object in which an umbral eclipse of the Sun will be seen is
in back of an object in which an umbral eclipse of the Sun will be seen is
![\begin{displaymath}
l = \frac{d}{2\tan [\theta/2]}
\end{displaymath}](img26.png)
![]() Synodic period of the Moon:
Synodic period of the Moon:
![]() days.
days.
![]() Nodal period of the Moon:
Nodal period of the Moon:
![]()
![]() Condition for repetition of eclipses:
Condition for repetition of eclipses:
![]() Angular momentum of an object (with mass m) moving with velocity
Angular momentum of an object (with mass m) moving with velocity ![]() a distance
a distance ![]() from the origin of a coordinate system:
from the origin of a coordinate system:
![]() Definition of vector angular velocity
Definition of vector angular velocity ![]() , such that
, such that
![]() ,
,
![]() Moment of inertia for uniform sphere of mass
Moment of inertia for uniform sphere of mass ![]() and radius
and radius ![]() :
:
![]() Definition of torque: causes change in angular momentum with time:
Definition of torque: causes change in angular momentum with time:
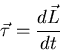
![]() The definition of a vector cross product:
The magnitude of a cross product is defined as follows. If
The definition of a vector cross product:
The magnitude of a cross product is defined as follows. If
![\begin{displaymath}
\left[
\begin{array}{ccc}
\hat{e}_x & \hat{e}_y & \hat{e}_z \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{array}\right]
\end{displaymath}](img47.png)
![]() Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the
Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the ![]() component of the vector, then the
component of the vector, then the ![]() component, etc.
component, etc.
![]() Centripetal acceleration: If an object moves in a circle of radius
Centripetal acceleration: If an object moves in a circle of radius ![]() with speed
with speed ![]() , it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
, it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
![]() The gravitational force: If two objects possessing masses
The gravitational force: If two objects possessing masses ![]() and
and ![]() are a distance
are a distance ![]() apart, there is an attractive force between them, the magnitude of which is
apart, there is an attractive force between them, the magnitude of which is
![]() The circular orbit equation. If
The circular orbit equation. If ![]() , and the orbit of
, and the orbit of ![]() about
about ![]() is circular, there is a relation between the radius of the orbit
is circular, there is a relation between the radius of the orbit ![]() , the orbital speed
, the orbital speed ![]() , and the mass
, and the mass ![]() which is called the circular orbit equation. It says
which is called the circular orbit equation. It says
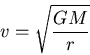
![]() ,
,
![]() and
and ![]() ,
,
![]() Kepler's 3rd Law:
Kepler's 3rd Law:
![]() Radioactive decay,
Radioactive decay,
![]() , where
, where ![]() is the unstable parent isotope,
is the unstable parent isotope, ![]() is the daughter isotope (product of the decay), and
is the daughter isotope (product of the decay), and ![]() is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
![]() Exponential decay law:
Exponential decay law:

![]() Equation for determining age of formation of rock from ratio of isotopes.
Equation for determining age of formation of rock from ratio of isotopes.

![]() Definition of density
Definition of density ![]()
![]() Escape speed from a planet
Escape speed from a planet
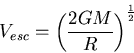
![]() root-mean-square (rms) molecular speed in a gas
root-mean-square (rms) molecular speed in a gas
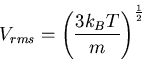
![]() Definition of the distribution function for molecular speeds
Definition of the distribution function for molecular speeds
![]() The Maxwellian distribution function
The Maxwellian distribution function
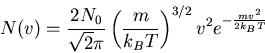
![]() Condition for retention of planetary atmosphere over geological timescales
Condition for retention of planetary atmosphere over geological timescales
![\begin{displaymath}
T_{eq} = \left[ \frac{(1-A)S_0}{\sigma}\right]^{\frac{1}{4}}
\end{displaymath}](img117.png)