29:50: Stars, Galaxies, and the Universe
Laboratory Project
Measurements of
Angular Sizes With a Telescope
June 21, 2004
I. Introduction
When sizes of astronomical objects are measured, it is almost always the case that an angular size is first measured, then converted to a diameter using knowledge of the distance to the object. The point of this exercise is to give a rough idea of how one can measure angular sizes, even roughly, through a telescope. This exercise has the added advantage of having the student actually look at some objects through the telescope, and extract some rough numbers.
This lab exercise does not require a formal writeup. Data taking, drawings, and calculations are to be entered on this form and handed to the teaching assistant. However, you need to preserve your results for later in the semester when you will measure angular sizes of other objects, then use known distances to determine their sizes (radii or diameters).
An important concept in this project is that of the magnification of a telescope. It is expressed as a number greater than one, indicates how much a bigger an astronomical object looks through the telescope than it would if viewed with the naked eye alone. Alternatively, the object looks like you are closer to it by a factor equal to the magnification. If your telescope has a magnification of 100X, the object looks like it would with the unaided eye if you were 1/100 of your actual distance. This is the way a telescope allows us to see an object up close.
The magnification is determined by the focal length of the telescope (the distance between the lens or mirror and the point where the light rays come to a point) F1, and the focal length of the eyepiece F2. The magnification of the telescope is then given by M=F1/F2.
II. Procedure
The procedure consists of estimating the angular sizes of objects viewed through the eyepiece of a Celestron 8 telescope. At least two eyepieces will be used. The first will have a fairly large field of view. The second will have higher magnification, and has a scale which allows you to fairly accurately measure small angles. A Celestron 8 has a focal length of 2000 millimeters.
We start by calibrating the observations with observations of the Moon. The Moon has an average angular diameter (the full angle subtended by the Moon) of about 31 arcminutes (remember 60 arcminutes = 1 degree). Your teaching assistant may give you the exact value on the night of the lab, but the accuracy of this measurement will not usually warrant such care.
(a). Put in an eyepiece with a focal length of 25
millimeters. What is the magnification
of the telescope with this eyepiece?
(b)
Put the Moon in the field of the telescope, and estimate the fraction of the
width of the field occupied by the Moon.
Discuss the value with your lab partners, and come up with a seems to be
a best value. Let R be the fraction of the
field of view occupied by the Moon,
expressed as a number between 0 and 1.0. Write down your value here:
..
(c)
The total angular width of the field of view of the
telescope with this eyepiece is then FOV=31/R arcminutes. Note that if you use a more exact value for
the angular diameter of the Moon, you
should use that value in calculating the FOV rather than 31 arcminutes. Put your value for the FOV here:
..
(d)
If you now change eyepieces to one with a shorter focal
length F2 (and thus a higher magnification),
the size of the field of view will be smaller by the ratio of the
magnification factors, or equivalently
by the ratio of the focal lengths of eyepieces. In other words, if the
field of view is determined to be 20 arcminutes with an eyepiece having a focal
length of 25 millimeters, it will have
a field of view of 10 arcminutes when an eyepiece of 12.5 millimeters is
used.
(e)
Take one of the shorter focal length eyepieces with a
scale on it. The scale is called a
reticle. Note the focal length. Calculate out what the FOV with this
eyepiece is. Do it! Write down value of the field of view
(FOV) here:
..
(f)
The reticle scale has a number of large tick marks,
separated by 5 small tick marks. Given
your result for part (e), write down
the angular spacing between the large and small tick marks. Use arcminutes or arcseconds (60 arcseconds
= 1 arcminute as appropriate. Record
your answer here:
(g)
Using the results from Part (f), measure the angular size of any feature you see on the surface of
the Moon . Use the Moon map given
below.
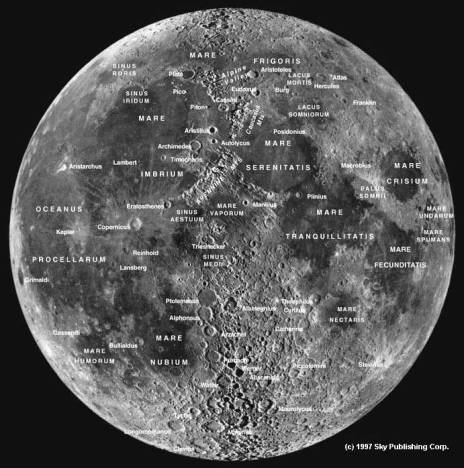
Record your observations in the table below. Before recording your final answer, you
might check that it makes sense given the Moon map. Do it!
Lunar Feature Measured
.
Angular Size (with units)
.
III.
More Procedure:
Observations of Binary Stars in Bootes.
Now we are going to observe a couple of double stars in the constellation of Bootes. They are Xi Bootes and Epsilon Bootes, also called (Pulcherimma, most beautiful in Latin). See the attached chart below to find them. Your teaching assistant will point out the Constellation of Bootes to you.
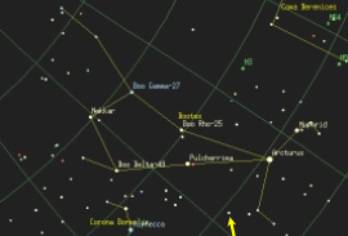
Xi Bootes
(h)
Use the reticle eyepiece to measure the angular separation
between the stars in Xi Bootes. Write
down your measurement here:
(i)
The distance to Xi Bootes is about 10 parsecs. The separation between the two stars is
S = DA, where D is the distance in parsecs,
and A is the angular separation in arcseconds. S is then given in units of astronomical units. Write down your work in the calculation on
blank parts of this form. Write down your
final result here:
(j)
Is the distance between the two stars you just calculated
the true distance, or is it just a lower limit to that distance? Describe your reasoning.
(k)
Finally, describe
the appearance of the two stars in this binary star system. Use an eyepiece that gives you the best
view, probably one with a still shorter
focal length. Comment on properties
such as the relative brightness and color of the two components. Describe it verbally here, and draw a sketch (if you feel so moved) in
blank parts of the form
.. The two stars are main sequence stars
of spectral type G8 and K4.
(l)
Find and observe the star Pulcherrima (Epsilon Bootes),
and describe its appearance. You will
probably have to use a high magnification (short focal length) eyepiece.
.
IV. Observation of the Great Globular Cluster in Hercules
Now lets use an angular size measurement to determine the diameter of another object. In the part of the sky between the constellation Bootes and the bright star Vega is the constellation of Hercules. A number of globular star clusters are found in Hercules, particularly the cluster M13. Globular star clusters are very important as clues to stellar evolution and the shape of the Milky Way galaxy. See the map of Hercules below. The green dots are globular stars clusters, and the one in the box is M13.

(m)
Using a 25 millimeter (or even longer focal length)
eyepiece, observe M13 and estimate its
angular diameter. Write down your
measurement here and any other comments on the appearance of the star cluster.
(n)
The distance to M13 is 21,000 light years or 6500
parsecs. Think about this distance as
you look at it. The diameter of M13 is
then given by the formula S=DA/206265,
where S is the diameter in parsecs, D is the distance in parsecs, and A is the angular diameter in
arcseconds. Calculate the diameter in
parsecs and light years. Use blank
parts of this form to carry out your calculation, and write down your answers here
..
Thats it!!!