


Next: About this document ...
29:61 General Astronomy
Fall 2004
Lecture 10 ...October 21,2004
Kepler's Laws, Radioactive Decay, Physics of Atmospheres
Just the facts, Ma'am
Orbits and Kepler's Laws
 Equations for an ellipse:
Equations for an ellipse:
In Cartesian coordinates:
 |
(1) |
where  is the semimajor axis,
is the semimajor axis, 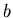 is the semiminor axis.
is the semiminor axis.
In polar coordinates 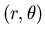 ,
,
 |
(2) |
where  is the semimajor axis and
is the semimajor axis and  is the eccentricity of the ellipse.
is the eccentricity of the ellipse.
Eccentricity in terms of  and
and 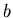 ,
,
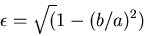 |
(3) |
 Kepler's 3rd Law:
Kepler's 3rd Law:
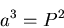 |
(4) |
 = semimajor axis of planetary orbit in astronomical units,
= semimajor axis of planetary orbit in astronomical units,  is the orbital period in years.
is the orbital period in years.
Radioisotope Dating
 Radioactive decay,
Radioactive decay,
 , where
, where 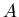 is the unstable parent isotope,
is the unstable parent isotope, 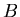 is the daughter isotope (product of the decay), and
is the daughter isotope (product of the decay), and 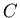 is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
 Exponential decay law:
Exponential decay law:
 |
(5) |
where 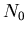 is the number of parent nuclei at
is the number of parent nuclei at  ,
, 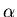 is the decay constant, and
is the decay constant, and  is the number of parent nuclei at time
is the number of parent nuclei at time  . The decay constant is related to the half life
. The decay constant is related to the half life  by
by
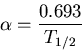 |
(6) |
 Equation for determining age of formation of rock from ratio of isotopes.
Equation for determining age of formation of rock from ratio of isotopes.
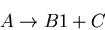 |
(7) |
where 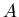 is the radioactive parent isotope,
is the radioactive parent isotope,  is the isotope of element
is the isotope of element 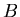 that is the daughter product of the decay reaction, and
that is the daughter product of the decay reaction, and  is the isotope of element
is the isotope of element 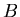 that is not the daughter product of the decay. Let
that is not the daughter product of the decay. Let 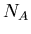 be the number of isotopes of
be the number of isotopes of 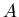 in a sample,
in a sample,  the number of isotopes of
the number of isotopes of  , and
, and  the number of isotopes of
the number of isotopes of  , then we have the following equation
, then we have the following equation
 |
(8) |
where 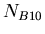 was the number of nuclei of isotope
was the number of nuclei of isotope  when the rock formed.
when the rock formed.
Physical Characteristics of the Planets
 Definition of density
Definition of density 
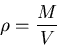 |
(9) |
where 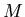 is mass and
is mass and  is volume. Units of density are kilograms/m
is volume. Units of density are kilograms/m . Typical densities of common substances and astronomical objects are:
. Typical densities of common substances and astronomical objects are:
- water: 1000 kg/m

- rock: 2900 - 3900 kg/m

- aluminum: 2700 kg/m

- brass: 8600 kg/m

- lead: 11300 kg/m

Physics of Planetary Atmospheres
 Escape speed from a planet
Escape speed from a planet
 |
(10) |
where 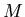 is the mass of the planet, and
is the mass of the planet, and 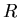 is its radius.
is its radius.
 root-mean-square (rms) molecular speed in a gas
root-mean-square (rms) molecular speed in a gas
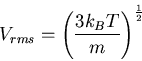 |
(11) |
where 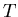 is the temperature (K), and
is the temperature (K), and  is mass of the molecule or atom in the gas.
is mass of the molecule or atom in the gas.
 Definition of the distribution function for molecular speeds
Definition of the distribution function for molecular speeds
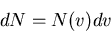 |
(12) |
is the differential number of molecules with speeds in the range
 .
.
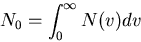 |
(13) |
where 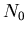 is the total number of molecules/m
is the total number of molecules/m .
.
 The Maxwellian distribution function
The Maxwellian distribution function
 |
(14) |
This distribution describes the true distribution for gases in planetary atmospheres, as well as most other astronomical gases.
 Condition for retention of planetary atmosphere over geological timescales
Condition for retention of planetary atmosphere over geological timescales
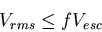 |
(15) |
where  is a number between 1/6 and 1/4.
is a number between 1/6 and 1/4.



Next: About this document ...
Steve Spangler
2004-10-22
![]() ,
,
![]() and
and ![]() ,
,
![]() Kepler's 3rd Law:
Kepler's 3rd Law:
![]() Radioactive decay,
Radioactive decay,
![]() , where
, where ![]() is the unstable parent isotope,
is the unstable parent isotope, ![]() is the daughter isotope (product of the decay), and
is the daughter isotope (product of the decay), and ![]() is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
is a particle which comes out as a result of the decay, such as beta particle (electron or positron), alpha particle (helium nucleus), or larger piece of a nucleus.
![]() Exponential decay law:
Exponential decay law:
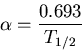
![]() Equation for determining age of formation of rock from ratio of isotopes.
Equation for determining age of formation of rock from ratio of isotopes.

![]() Definition of density
Definition of density ![]()
![]() Escape speed from a planet
Escape speed from a planet

![]() root-mean-square (rms) molecular speed in a gas
root-mean-square (rms) molecular speed in a gas
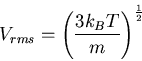
![]() Definition of the distribution function for molecular speeds
Definition of the distribution function for molecular speeds
![]() The Maxwellian distribution function
The Maxwellian distribution function

![]() Condition for retention of planetary atmosphere over geological timescales
Condition for retention of planetary atmosphere over geological timescales