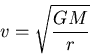Next: About this document ...
29:61 General Astronomy
Fall 2004
Lecture 9 ...September 27,2004
Vector Cross Products, Newton's Laws, the Gravitational Force
Just the facts, Ma'am
 The definition of a vector cross product:
The magnitude of a cross product is defined as follows. If
The definition of a vector cross product:
The magnitude of a cross product is defined as follows. If
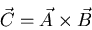 |
(1) |
then the direction of
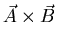 is given by the right hand rule.
The magnitude of
is given by the right hand rule.
The magnitude of
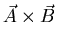 is given by
is given by
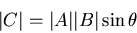 |
(2) |
where 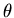 is the angle between the two vectors. Another way of expressing it as follows. Draw up an array
is the angle between the two vectors. Another way of expressing it as follows. Draw up an array
![\begin{displaymath}
\left[
\begin{array}{ccc}
\hat{e}_x & \hat{e}_y & \hat{e}_z \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{array}\right]
\end{displaymath}](img6.png) |
(3) |
For each component, knock out the column corresponding to that coordinate, and form the product of the remaining terms. The result for the vector is
 |
(4) |
 Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the
Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the  component of the vector, then the
component of the vector, then the 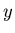 component, etc.
component, etc.
Newton's Laws of Motion
- An object in motion remains in motion with constant vector momentum
 , unless acted upon by an external force. An object at rest has zero momentum, and therefore remains at rest.
, unless acted upon by an external force. An object at rest has zero momentum, and therefore remains at rest.
- If a force acts on an object, its momentum changes according to
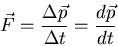 |
(5) |
If the mass of the object acted upon stays constant, this simplifies to
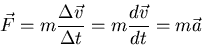 |
(6) |
where 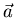 is the acceleration.
is the acceleration.
- If an object A exerts a force on B, B exerts a force on A which is equal in magnitude and opposite in direction to that exerted by A on B. Rather lyrically said, ``to every action there is an opposite and equal reaction''.
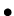 Centripetal acceleration: If an object moves in a circle of radius
Centripetal acceleration: If an object moves in a circle of radius 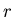 with speed
with speed 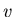 , it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
, it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
 |
(7) |
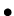 The gravitational force: If two objects possessing masses
The gravitational force: If two objects possessing masses 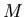 and
and  are a distance
are a distance 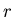 apart, there is an attractive force between them, the magnitude of which is
apart, there is an attractive force between them, the magnitude of which is
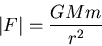 |
(8) |
where 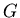 is the gravitational constant,
is the gravitational constant,
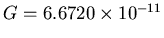 N-m
N-m -kg
-kg .
.
 The circular orbit equation. If
The circular orbit equation. If 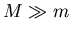 , and the orbit of
, and the orbit of  about
about 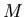 is circular, there is a relation between the radius of the orbit
is circular, there is a relation between the radius of the orbit 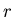 , the orbital speed
, the orbital speed 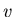 , and the mass
, and the mass 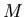 which is called the circular orbit equation. It says
which is called the circular orbit equation. It says
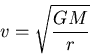 |
(9) |



Next: About this document ...
Steve Spangler
2004-09-27
![\begin{displaymath}
\left[
\begin{array}{ccc}
\hat{e}_x & \hat{e}_y & \hat{e}_z \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{array}\right]
\end{displaymath}](img6.png)
![]() Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the
Remember that in a vector equation, the equation must be satisfied component by component, in other words, you must satisfy the equation for the ![]() component of the vector, then the
component of the vector, then the ![]() component, etc.
component, etc.
![]() Centripetal acceleration: If an object moves in a circle of radius
Centripetal acceleration: If an object moves in a circle of radius ![]() with speed
with speed ![]() , it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
, it undergoes a centripetal acceleration which points toward the center of the circle and has a magnitude
![]() The gravitational force: If two objects possessing masses
The gravitational force: If two objects possessing masses ![]() and
and ![]() are a distance
are a distance ![]() apart, there is an attractive force between them, the magnitude of which is
apart, there is an attractive force between them, the magnitude of which is
![]() The circular orbit equation. If
The circular orbit equation. If ![]() , and the orbit of
, and the orbit of ![]() about
about ![]() is circular, there is a relation between the radius of the orbit
is circular, there is a relation between the radius of the orbit ![]() , the orbital speed
, the orbital speed ![]() , and the mass
, and the mass ![]() which is called the circular orbit equation. It says
which is called the circular orbit equation. It says