High-dimensional Simulations of Collisionless Shocks

Collisionless shocks play an important role in the heliosphere by irreversibly converting the energy of supersonic plasma flows into other forms, including heat, energetic particle acceleration, and electromagnetic field energy. At the forefront of research efforts on collisionless shocks is the question of how the kinetic instabilities that arise naturally in the shock transition impact the stability of the shock, the energization of particles, and the ultimate partitioning of energy among different forms through the shock. For example, the high-energy particles accelerated at shocks associated with solar flares and coronal mass ejections from the Sun pose a significant extreme space weather threat to the spaceborne technology upon which our nation's economy and society depend, such as satellite communication and GPS navigation. The development of cutting-edge simulation codes that model the shock dynamics in the six-dimensional phase space (3D3V, three dimensions of physical space and three dimensions of velocity space) of collisionless plasmas is critical to developing a predictive capability for the energization of particles as collisionless shocks.

Here we aim to extend the application of the continuum Vlasov solver in the Gkeyll suite of simulation codes, developed by the Princeton Plasma Physics Laboratory, to the higher dimensionality essential to capture the key physics of kinetic instabilities at quasiparallel collisionless shocks. Previous investigations have used Gkeyll successfully to model quasiperpendicular collisionless shocks in lower dimensions (1D2V and 1D3V), but for quasiparallel shocks capturing the physics of kinetic instabilities requires minimally modeling the dynamics in at least two spatial dimensions (2D3V). This project aims to achieve the successful modeling of a quasiparallel collisionless shock to provide an unprecedented view of the phase-space dynamics and energetics using a continuum Vlasov solver, thereby providing our nation a valuable new tool to predict the acceleration of high-energy particles that pose a threat to our nation's spaceborne technological assets.

Gkeyll Performance on Perlmutter

We have performed strong and weak scaling tests using multiple GPUs on Perlmutter, the flagship system at the Department of Energy's National Energy Research Scientific Computing Center (NERSC). Each Perlmutter node contains four NVIDIA A100 GPUs. The strong scaling shows the performance for a (Nx,Ny,Nv^3)=(32,32,16^3) problem using quadratic (p=2) basis functions in the discontinuous Galerkin scheme using N_GPU= 4, 16, 64, 128 GPUs, with performance eventually degrading due to insufficient compuational load per GPU at the largest GPU numbers. The weak scaling starts with a (Nx,Ny,Nv^3)=(16,16,16^3) with p=2 basis functions on a single GPU, and scales up to N_GPU= 4, 16, 64, 256, 1024 GPUs with the size of the computational gird increasing by the factor N_GPU for each case. Here we see the time per step increasing to 1.9 times the ideal performance at the largest run with 1024 GPUs.

Previous Collisionless Shock Studies with Gkeyll

Gkeyll has been used successfully to model a perpendicular collisionless shock in 1D2V, highlighting its ability to identify the acceleration of ions by the shock-drift acceleration mechanism. Subsequently, Gkeyll modeled a quasiperpendicular collisionless shock in 1D3V, illustrating how it enables multiple populations of ions to be isolated and studied, including:

• incoming ions within the incoming ion beam,
• accelerated ions that are reflected by the shock, accelerated, and then pass downstream,
• backstreaming ions that are reflected by the shock, accelerated, and then pass downstream.

These studies have demonstrated the power of the continuum velocity-space representation in the Vlasov solver to determine the underlying kinetic plasma physics mechanisms that govern the energization of plasma particles through a collisionless shock.

Perpendicular Collisionless Shock in 1D2V

The initial Gkeyll simulations of a perpendicular collisionless shock were reported in
Juno, J., et al. J. Plasma Phys., 87, 905870316 (2021).
A Field-Particle Correlation Analysis of a Perpendicular Magnetized Collisionless Shock
Below we present a few key results from this first application of the field-particle correlation technique of collisionless shocks, exploiting the low noise velocity distribution functions from the Gkeyll Vlasov code.

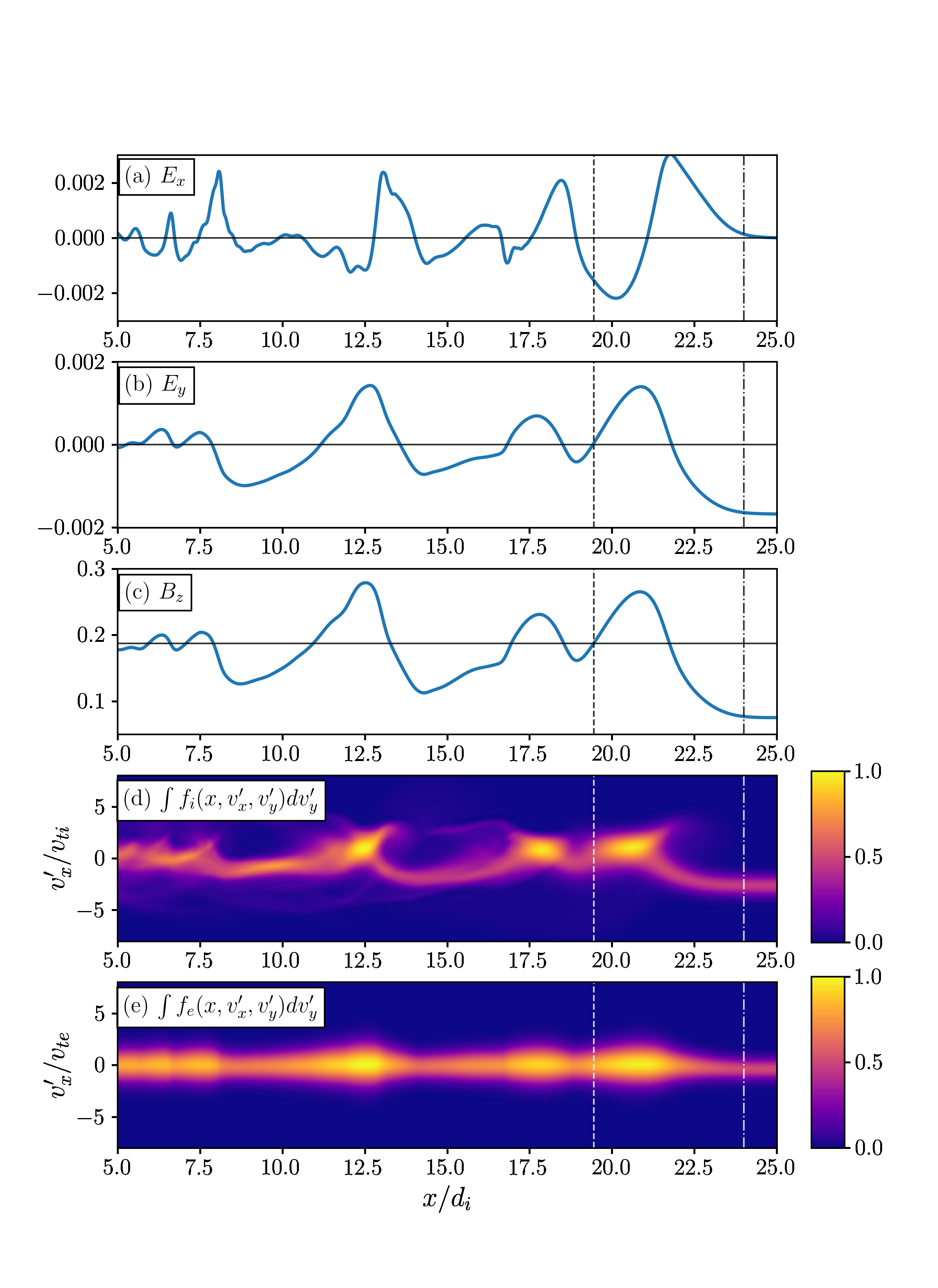
We used Gkeyll to simulate an exactly perpendicular collisionless shock with upstream parameters (M_A,θ_Bn,β_i,β_e)=(5,90°,1.3,0.7), plotting below the shock profile at tΩ_i=11 in the downstream rest frame (the same as the simulation frame, denoted by primed variables). The shock transition is highlighted between the vertical dot-dashed line and dashed line, showing (c) the typical foot-ramp-overshoot structure in the transverse magnetic field B_z. One can see in panel (d) the reflected ion component with v'_x > 0 at around x/d_i ~ 21.5.

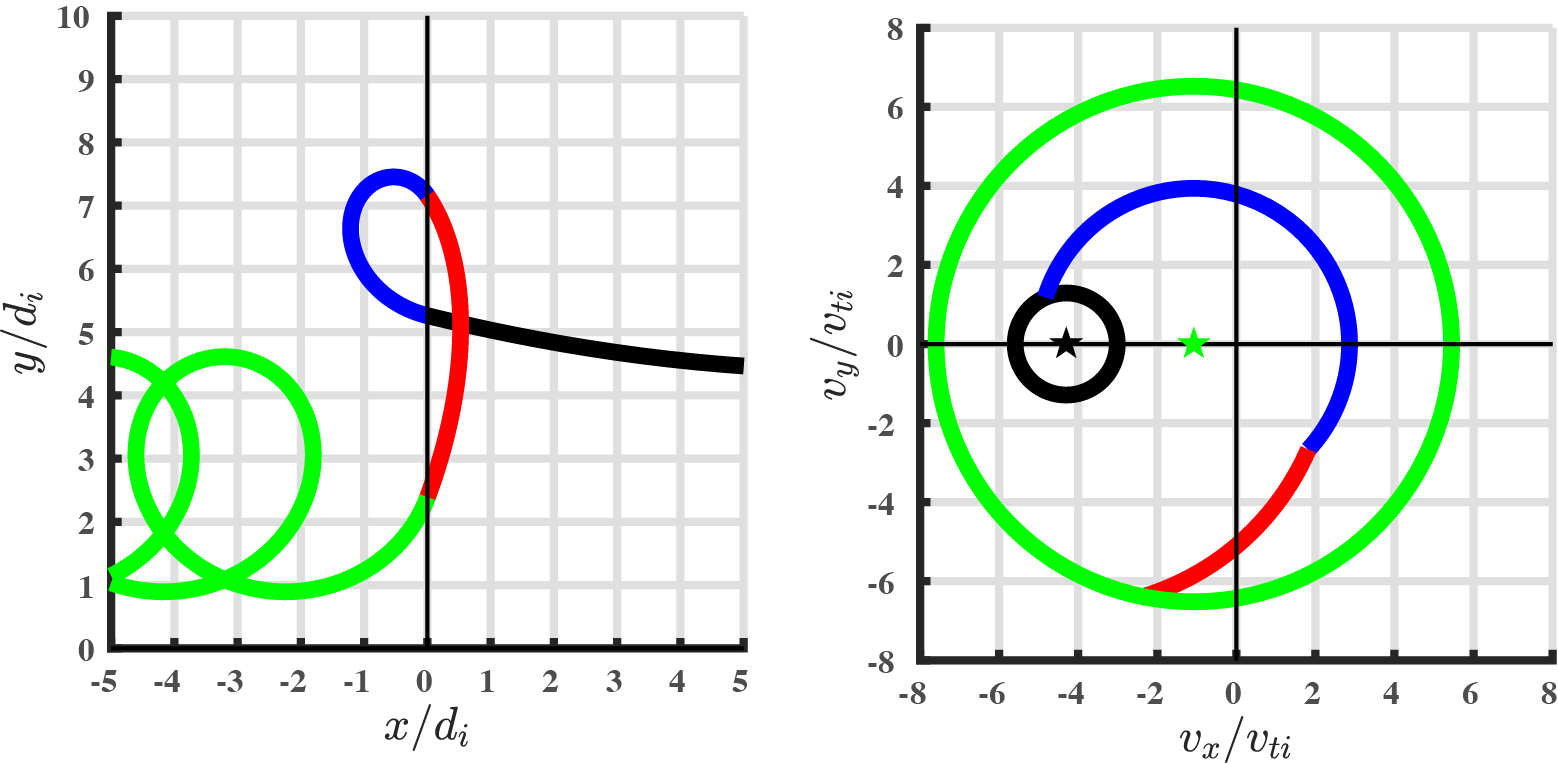
To intepret the features of the ion velocity distribution in velocity space, particulkarly the reflected ions that undergo the process of shock-drift acceleration, we plot below the trajectory of a typical reflected ion encountering a jump in the transverse magnetic field in (left) (x,y) space and (right) (v_x,v_y) space in the shock-rest frame of reference. Upon reflection at the shock front (due to the jump in transverse magnetic field B_z), the ion undergoes shock-drift acceleration by the motional electric field (E_y > 0) in the red segment of its trajectory, moving away from the origin of velocity space.

To interpret the ion velocity distribution in the Gkeyll simulation, we plot below (lower left) the ion velocity distribution at x/d_i = 22.9 in the shock foot, showing the incoming ion beam at (v_x/v_ti,v_y/v_ti)=(-4.4,0) and an arc-shaped distribution of reflected ions centered at (v_x/v_ti,v_y/v_ti)=(0,-6). Taking the field-particle correlation with the motional electric field E_y yields (lower right) the velocity-space signature of shock-drift acceleration, the blue red arc at (v_x/v_ti,v_y/v_ti)=(0,-6), indicating that the reflected ions dominate the ion energization at this position in the foot, due to the process of shock-drift acceleration. The top row shows a Liouville mapping prediction of the ion velocity distribution and field-particle correlation by following ion trajectories in modeled strucutre of the shock electromagnetic fields, showing clearly (upper right) that the velocity-space signature of shock-drift acceleration coincides with the reflected segment of the ion trajectory (red segement on previous plot).

Together, these results illustrate the power of the continuum Vlasov representation of the physics using the Gkeyll solver, which provides essentially noise-free calculations of the ion velocity distribution (as well as the electron velocity distribution, not shown here but discussed in the paper) at each point in the physical(x,y) space of the domain. This capability is critical to apply the field-particle correlation technique to explore the ion energization at collisionless shocks.

Oblique Collisionless Shock in 1D3V

A follow-up paper used Gkeyll simulations to explore the ion energization in a quasiperpendicular collisionless shock at an oblique angle of 45 deg, reported in
Juno, J., et al. Astrophys. J., 944, 15 (2023).
Phase-space Energization of Ions in Oblique Shocks
This study illustrates the power of the continuum Vlasov representation of the Gkeyll solver to identify the different ion populations in the shock transition, including the incoming ion beam, shock-drift accelerated ions, and backstreaming ions.

We used Gkeyll to simulate a quasiperpendicular collisionless shock with upstream parameters (M_A,θ_Bn,β_i,β_e)=(8.3,45°,1.3,0.7), plotting below the shock profiles of the (a) electric field and (b) magnetic field at tΩ_i=8 transformed to the shock-rest frame of reference. We also plot (c) the ion velocity distribution in (x,v_x) phase space and two reduced 2V views of the 3V velocity distribution in (d) (v_x,v_y) velocity space and (e) (v_x,v_z) velocity space at position x/d_i = 16 at the transition from the shock foot to the shock ramp.

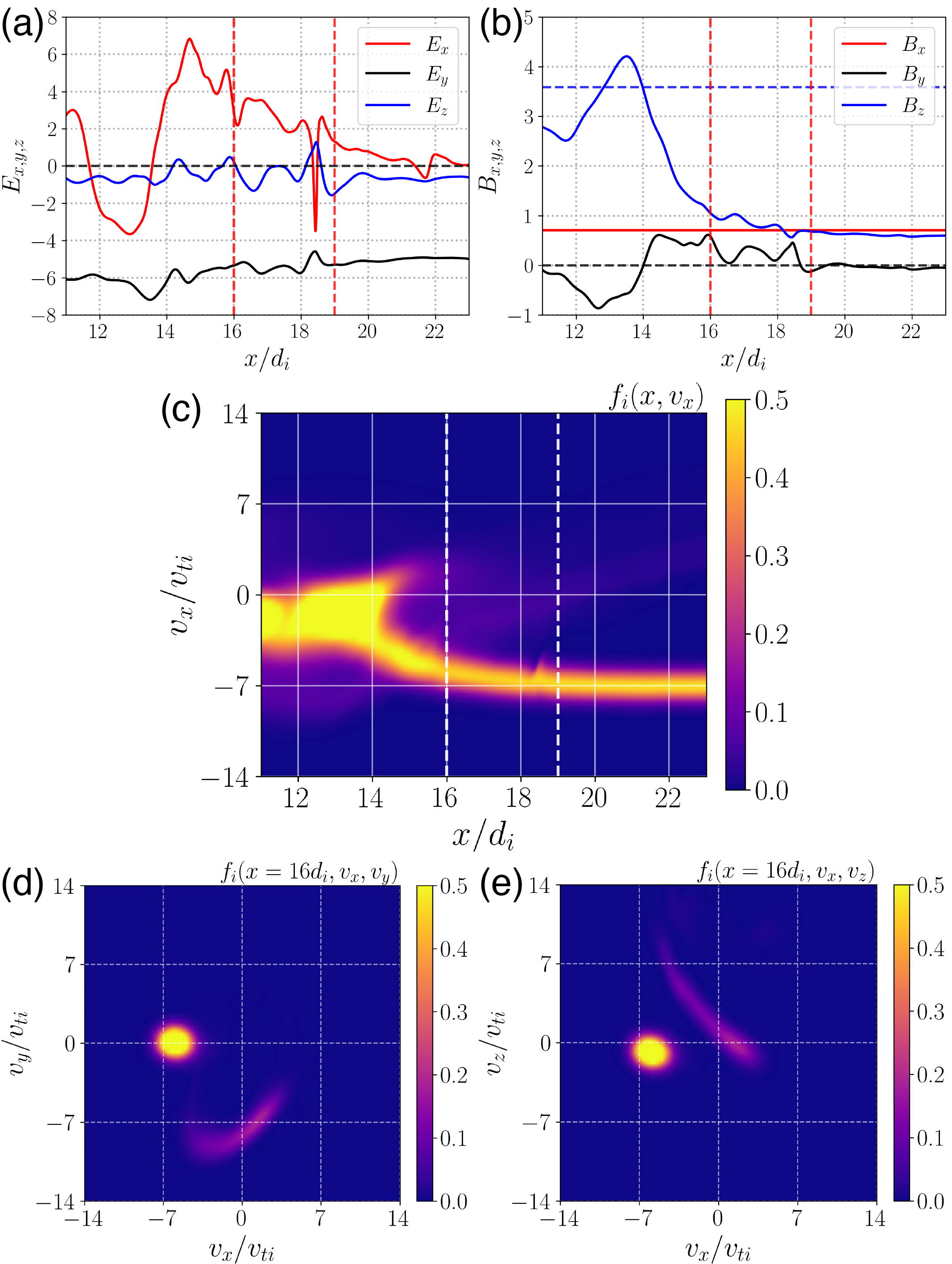
The essentially noise-free calculations of the ion velocity distribution by Gkeyll enable us to explores even logarithmically small populations of ions in the shock transition, as illustrated in the plot below. In particular, the right two columns of the plot present the two reduced 2V views of the velocity distribution (c) (v_x,v_y) and (g) (v_x,v_z). In (g), this view shows that there are in fact three separately identifiable ion populations:
(i) the incoming ion beam at (v_x/v_ti,v_y/v_ti)=(-7.3,0)
(ii) the shock-drift accelerated ions given by the diagnoally tilted population at (v_x,v_z)=(0,5)
(iii) the backstreaming ions at (v_x,v_z)=(10,3).
The field-particle correlation analysis shows that in the shock foot, we see (h) that the reflected ions undergoing shock-drift acceleration dominate the ion energization by the motional electric field E_y.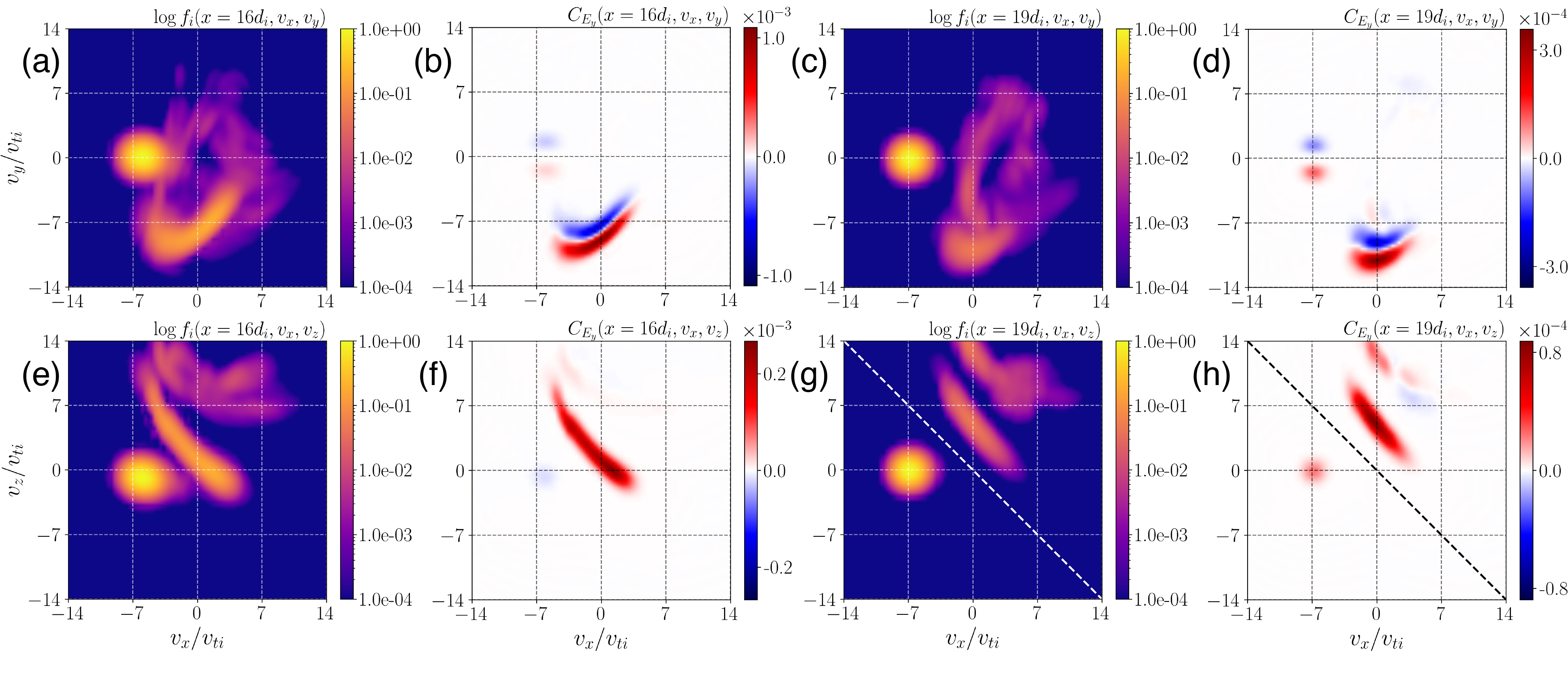

To definitely determine that the third population of ions seen in (g) in the figure above are indeed escpaing along the magnetic field back upstream as backstreaming ions, we plot below an example trajectory of one of these ions in (a) (x,z) and (c) (x,y) physical space and (b) (v_x,v_z) and (d) (v_x,v_y)'velocity space. One can see in (b) that, as the ion reflects twice from the shock transition [most easily seen in panel (c)], the ion stairsteps its way to higher v_z, enabling it to gain enough velocity to escape upstream along the magnetic field.

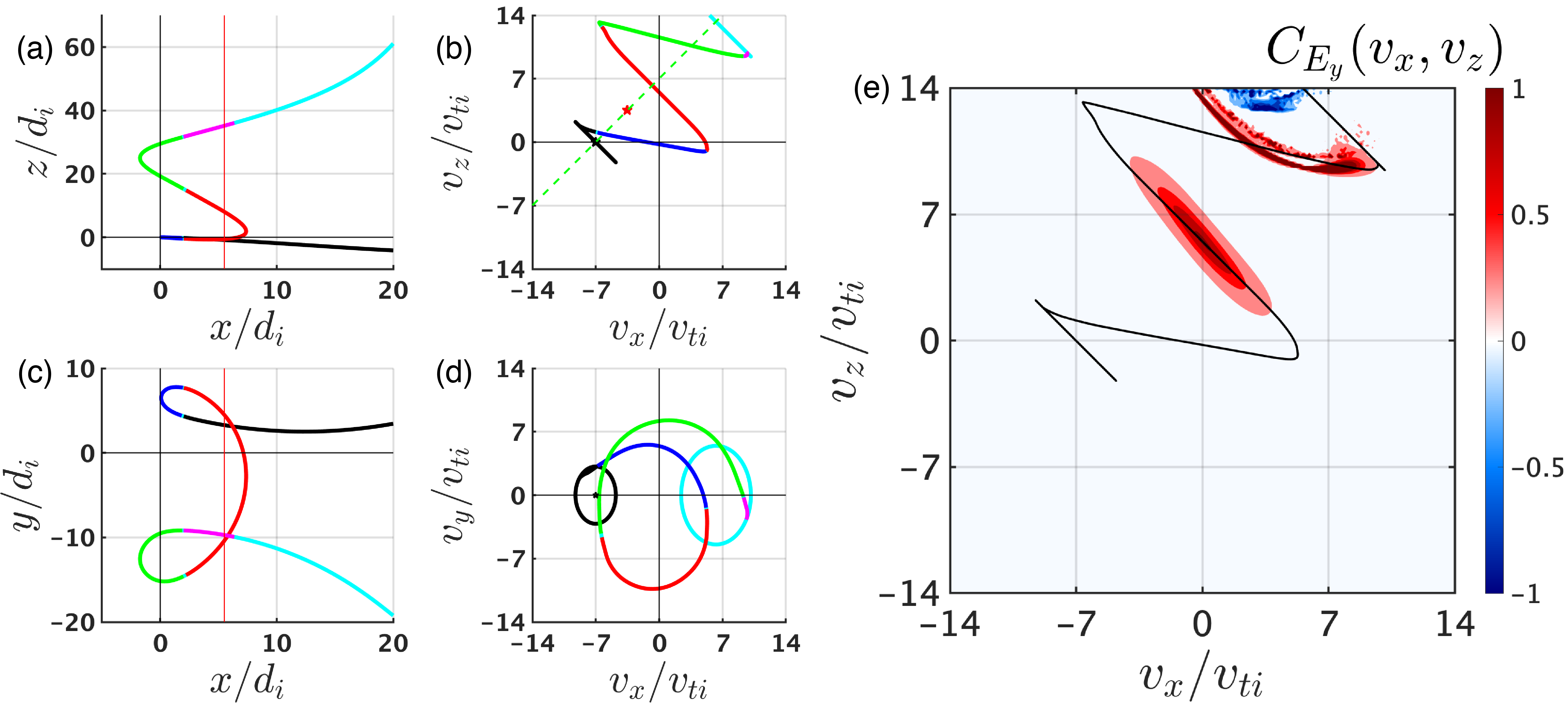
This example show the power of the continuum Vlasov representation of Gkeyll, enabling us to identify clearly the very diffuse population of backstreaming ions and determine their process of acceleration and escape.

High-Dimensional Simulations of Collisionless Shocks Using Gkeyll

A major topic at the forefront of the study of collisionless shocks is how kinetic instabilities that naturally arise due to the very non-Maxwellian ion velocity distributions in the shock transition impact the resulting energization of both ions and electrons. However, resolving these instabilities in kinetic simulations requires the shock to be simulated in at least two spatial dimensions (2D) as well as the three dimensions of velocity space (3V). Such 2D-3V simulations are computationally costly, and modeling them with Gkeyll Vlasov solver remains a primary computational challenge to be tackled in this project.

We currently are pursuing the use of two leading supercompuating facilities to model both quasiperpendicular and quasiparallel shocks in 2D-3V Gkeyll simulations. We aim use NSF's Delta GPU supercomputer at the NCSA to simulate a quasiperpendicular shock in 2D3V through an NSF ACCESS allocation. We aim use DOE's Perlmutter GPU supercomputer at the NERSC to simulate a quasiparallel shock in 2D3V through an ERCAP allocation. As we generate results from these allocations, results willbe presented here.