29:50 Modern Astronomy
Fall 2002
Lecture 12 ...October 2, 2002
The Energy Source of the Sun and Stars
Where do the Sun and stars get their energy from?
1. Stellar Powerplants
Let's get quantitative. What is the physical unit of power? Ans: the Watt.
Power 
energy/time. In the metric system of units, the unit of energy is the
Joule. 1 Watt = 1 Joule/sec. Watts are familiar to us from powers of light bulbs.
The power output of the Sun is
Watts. This is an unfathomably large number. What makes it particularly
incredible is that it has been keeping up this luminosity over geological timescales, i.e.
several billion years. That means the Sun has a huge energy source. What is it?
2. An incorrect but illustrative answer Most energy sources we are used to involve chemical reactions which convert one compound into another, and energy is given off in the process. This is true of all burning processes such as burning gasoline, burning coal, etc. In chemical reactions we have something like :
In this we have two molecules come together on the left hand side of the equation, produce a new molecule + energy on the right hand.
A measure of ``bang for the buck'' is how many Joules of energy you get for each kilogram of reactants on the left hand side.
As it says in the book, a typical number for chemical reactions is about a million
Joules per kilogram. Higher for nitroglycerine, lower for peat moss, but in this ballpark.
Therefore 
.
Note that a kilogram of liquid fuel is about one liter.
Let's do an interesting calculation, which was first done in the middle of the last
century. Assume that the Sun obtains its energy by some sort of chemical reaction. This
reaction proceeds at a rate that releases 
W by converting
the Sun from reactants to reaction products. How long could it keep this up?
Use the equation E = PT, where E is the energy (Joules), P is the power (Joules/sec) and T is the time (seconds) you can keep this up. Therefore the time (which is what we want) is:
What is P? We know that, it is the luminosity of the Sun = Watts.
What is the total energy content of a big ball like the Sun?
Joules.
Therefore 
seconds.
Question for audience; Is that good enough? How long does that represent?
3. Nuclear Reactions in the Center of the Sun
We need to find another, vastly more effective mechanism for energy generation. Let's
look at the structure of the Sun.
Transparency with structure of the Sun (see Figure 17-1 of book).
As we go deeper in the Sun, the density of the Sun goes up, and the temperature
goes up. Mathematical models of the Sun's interior indicate that in the innermost
core, densities reach nearly 200 grams/cm 
, and the temperature is about 15 million Kelvin.
At these temperatures, nuclear fusion reactions can occur, and at these densities they occur a lot. A good example of a nuclear fusion reaction (a change in atomic nuclei) is
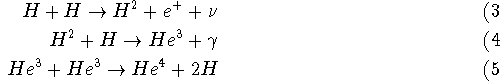
We can write this in shorthand as 
, it is called the proton-proton cycle.
It is a nuclear fusion reaction because the nuclei of the atoms are involved.
4. So What?
What does this have to do with the prodigious energy requirements of the Sun? If one
adds up the mass on the left hand side of the equation , one finds
that there is about 0.7 % mass than the right hand side of the equation. We have:
Mass of 4 hydrogen atoms: 
kilograms (atoms are little things)
Mass of 1 helium atom: 
kilograms
difference: 
kilograms.
It is small but measurable, and definitely there.
So what? Einstein's famous relation between mass and energy says mass can be changed into energy and vice-versa. The relation relating the two is
where c is the speed of light.
Nuclear fusion reactions can be incredible sources of energy. Example: take
1 kilogram of hydrogen. If we burned it, we'd get about 
Joules of energy. How
much from fusion reactions? If 1 kilogram of hydrogen proton- proton
cycle, you get 993 grams = 0.993 kilograms of helium. 0.007 kilograms has been converted
into energy. Therefore
Joules!
Summary in words. Link to the Manhattan Project.