29:50 Modern Astronomy
Fall 2002
Lecture 31 ...December 2, 2002
Cosmology
Watch the skies! Watch the skies!
At 8PM, Orion is rising in the southeast.
If up before dawn, you can now see Arcturus in the morning (predawn) sky.
In constellation of Cetus, is the star 
Ceti...spectral class G8 dwarf
, 3.49 parsecs away.
Picture of galaxy. Spiral Galaxy
Last time I discussed how rotation curves of galaxies showed that most of
the mass is in the form of dark matter, of unknown form.
We can get confirmation of this by observation of rich clusters of galaxies.
Picture of Coma cluster of galaxies. Coma Cluster
These galaxies are seen to be moving around under the force of their mutual gravity.
A discovery of the last couple of decades is that they are moving in an atmosphere of extremely hot gas, with temperatures of millions of degrees.
X-ray emitting gas in Hydra cluster. X-ray emitting gas in Hydra cluster
The amount of mass in this x-ray emitting gas is more than that in the stars in the galaxies!
#3 picture of galaxies & x-ray emitting gas. Galaxies and X-Ray Emitting Gas
To confine gas with that high a temperature, a strong gravitational field is required. That means
a lot of mass. When astronomers do the arithmetic they find the following.
Picture with gravitational lensing arcs Gravitational Lensing
Cosmology
Cosmology deals with questions such as how hold the universe is, what it will be like in the remote future, and what conditions were like in the beginning.
The discovery which led to the realization that the universe
had a beginning is Hubble's Law, which I have discussed as the only way of
determining distances to distant galaxies.
The precise value of the Hubble constant is currently believed to be about 70 kilometers
per second per Megaparsec.
Hubble's Law has a number of major consequences.
First It shows that the universe is expanding, or getting bigger with
time. Every second, the distance between us and every other galaxy is getting bigger, so the
universe is expanding. An analog of this is shown in Figure 23-35 of the textbook,
which shows the same thing applied to raisins in a loaf of bread.
The Second major consequence of Hubble's Law is the physical significance of Hubble's constant. It is nothing other than the reciprocal of the time since the expansion started. Stated somewhat differently, we now see all galaxies moving away from us. If we ran the film backwards, we would see the galaxies coming nearer and nearer, until eventually everything was on top of everything else.
The fact that the Hubble constant is related to the age of the universe can
be illustrated in a very simple, and equivalent way. Let's imagine we are
standing on a desert lake bed and we see cars driving away from us in all directions.
Blackboard diagram with cars moving away.
Furthermore (in analogy with the true Hubble's constant) we see that the further away they are the faster they are moving; the cars one mile away are driving at 60 miles per hour, those two miles away are driving at 120 miles per hour, and those three miles away are driving at 180 miles per hour.
It is clear from this observation that in the past, cars were much closer to you (and to each other) than they are now. You can then calculate how long ago the cars were at the point where you are now standing. In the case of the cars at one mile, you known that an object driving 60 miles per hour is going at a mile a minute. Thus is would have been ``here'' one minute ago. The car two miles away is receding at twice the speed, but has twice the distance to travel. It turns out it would have been at your position one minute ago as well. And so on. You would conclude that there was an infinite concentration of cars one minute ago.
You would be able to deduce the time since this concentration from the value of the ``Hubble'' constant. If the ``Hubble constant'' were half as large a value, i.e. 30 miles per hour per mile, the time since the expansion of the cars would be twice as long.
Let's work out the age of the universe from Hubble's constant. We have
,
so 
must have units of sec 
. What is this time, and what does it physically
represent?
So 
These are interesting numbers. First, it shows that the universe as a whole is
not vastly older than the solar system with an age of 4.5 billion years.
Second, the answer ``makes sense'' in that it is in the range of the oldest
objects we know of in astronomy.
Question for audience: what are the oldest objects we have discussed
in class?
The third point is that it is something of a tight fit. In the case of 
the reciprocal of the Hubble constant, the upper limit to the age of the universe,
is 10 billion years. There are objects which we believe are older than that.
Obviously the universe must be older than the oldest discrete objects, so either
the Hubble constant must be lowered, or we have made some mistake in determining
the ages of these ``oldest objects''.
Let's talk about exactly what this timescale represents. It is illustrated in Figure
26.13 of the text.
Figure 26.13
This shows that in the past the universe was much more compact than it is now.
What about the future? The possibilities are shown in Figure 26.12. Choose one!
Figure 26.12.
Two Points To Be Made
(1) The idea of the expanding universe can be illustrated with a number of toy analogs,
such as an expanding balloon.
Demonstration with expanding balloon.
(2) There is no center to the universal expansion. This is not intuitive, but that's the
way it is! Every observer in the universe would see galaxies expanding away from it
in all directions. Sort of an explanation is given later.
If Cosmology is to be a branch of physical science, there must be an underlying mathematical structure with quantitatively testable predictions.
There are two things going on in the universal expansion. (1) Galaxies are flying apart due to the universal expansion and (2) the force of Gravity is acting to pull them back together again. The story of the universe is the story of a competition between the universal expansion and gravity.
General Relativity
The best theory of gravity is General Relativity, a theory previously encountered to
describe Black Holes. There are two components of GR. (1) Dynamics of systems takes place
in a Four Dimensional Spacetime. (2) Mass induces warping or curvature of spacetime.
In some physical contexts, this curvature becomes pronounced, and space and time become inextricably linked or ``coupled''. An example we have seen is Black Holes. A second important example is the universe as a whole.
When we look on cosmological scales, on distances 
, you
cannot just view the universe as three dimensional, with time as a parameter. The
universe exists as 4D entity with strong curvature effects. You can't even qualitatively
understand what is going on if you stick to a 3D view.
An analogy The surface of the Earth as a 2D surface embedded in a 3D space. Locally, it looks purely 2D. On scales of the size of the Earth, the 3D nature is unavoidable.
Let's talk about Cosmology from the viewpoint of General Relativity.
Mass warping of spacetime (curvature). This is described by
Einstein's equation.
How do we solve the Einstein equation for the universe as a whole? You can't. You have to make some approximations which simplify the mathematics to the point where you can get some solutions to the equations. One of the primary ones is to assume a Friedmann Universe, in which the real universe is replaced by a paté with the same density. This then leads to a equation for the radius of curvature of the universe which is solvable (don't get hysterical; we are not going to solve this in this class!)
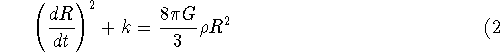
where R is the radius of curvature, 
is the mean density of matter in the universe,
and k is a parameter which the universe chose and determines the nature of the solutions.
This parameter can be negative, positive, or zero. It determines the nature of the solutions.
Figure 26.12 of text.
The value of k, and the correct solution in Figure 26.12, is determined by the
ratio of the density of matter in the universe to the critical density 
.
For the values of the Hubble constant we have been discussing, is about 
kilograms per cubic meter.
Comments on the cosmic deceleration parameter.