AstroGK Code Validation
Linear Laplace-Fourier Transform Solution
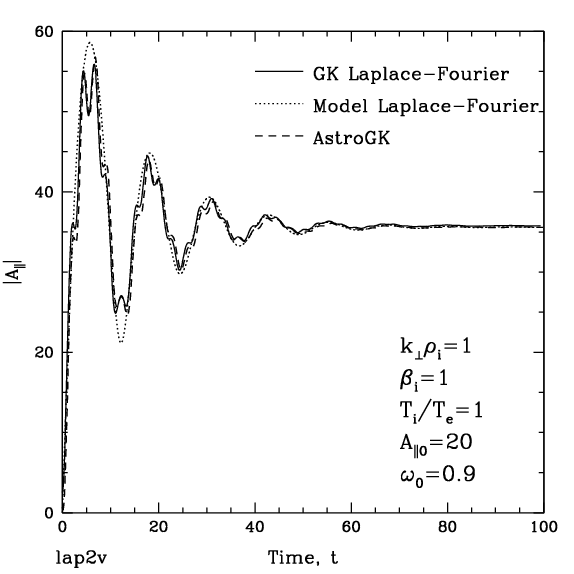
The amplitude response of the driven linear gyrokinetic system can be compared with an analytical Laplace-Fourier transform solution, given by \eqref{eq:lfgk} in \appref{app:lfgk}. In \figref{fig:laplace}, we plot this Laplace-Fourier solution of the gyrokinetic system with $\delta B_\parallel=0$ (solid line) and the output of \T{AstroGK} (dashed line). Parameters for the run are $k_\perp \rho_i=1$, $\beta_i=1$, and $T_i/T_e=1$; the system is driven with amplitude $A_{\parallel 0}=20$ at frequency $\overline{\omega}_0=0.9$. From the linear gyrokinetic dispersion relation with $\delta B_\parallel=0$, the frequency and damping rate for these parameters are $\overline{\omega}=1.4057$ and $\overline{\gamma}=0.073004$. The run parameters are \T{ntheta}$=32$, \T{ngauss}$=4$, \T{negrid}$=32$, and $\Delta t=0.16$; these choices achieve a converged result with minimal computational effort. Collision frequencies are $\nu_i=\nu_e=2 \times 10^{-2}$. The close agreement of the solid and dashed lines in \figref{fig:laplace}---faithfully reproducing even the small amplitude, high-frequency oscillation---demonstrate the ability of the \T{AstroGK} to accurately model a driven linear gyrokinetic system.
The model Laplace-Fourier transform solution, derived in \appref{app:lfmod}, is a more simple model than the gyrokinetic system but is useful for determining the effective frequency and damping rate for a given linear mode. The time dependence determined by \eqref{eq:lfmod} is plotted (dotted line) in \figref{fig:laplace} for the fitted values $\omega_0=0$, $\overline{\omega}=1.406$, $\overline{\gamma}=0.073$, and $S_0=18.2$. Note that fitting the oscillation of the solution at the beat frequency $|\omega-\omega_0|$ allows a precise determination of the resonant frequency. The fractional error in the damping rate is larger, in particular due to the difficulty of fitting the exponential decay in the presence of the higher frequency oscillations arising in the gyrokinetic system---compare the difference between the simple model (dotted line) and the gyrokinetic solution (solid line). Estimating the error in the frequency and damping rates based on these fits, we determine by this method values of $\overline{\omega}=1.406 \pm 0.004 $ and $\overline{\gamma}=0.073 \pm 0.003$.
|
Linear Frequencies and Damping Rates
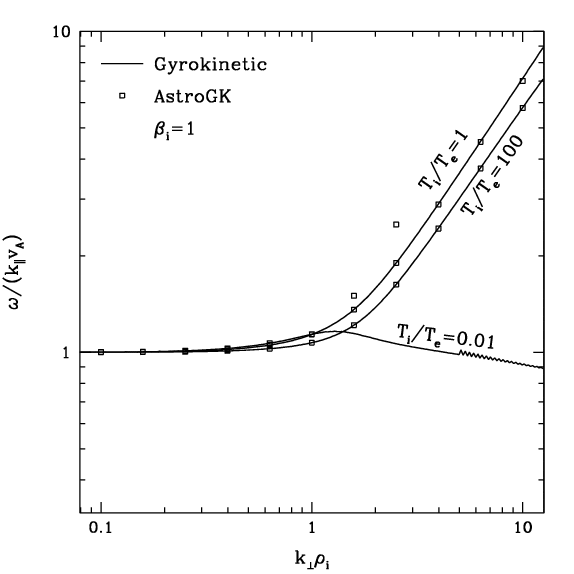
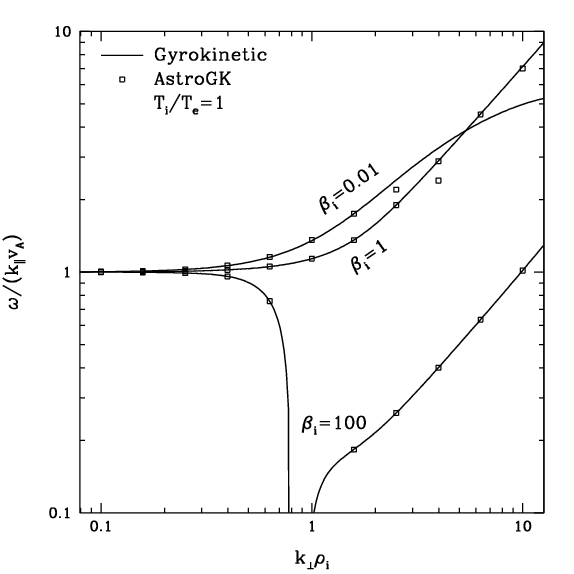
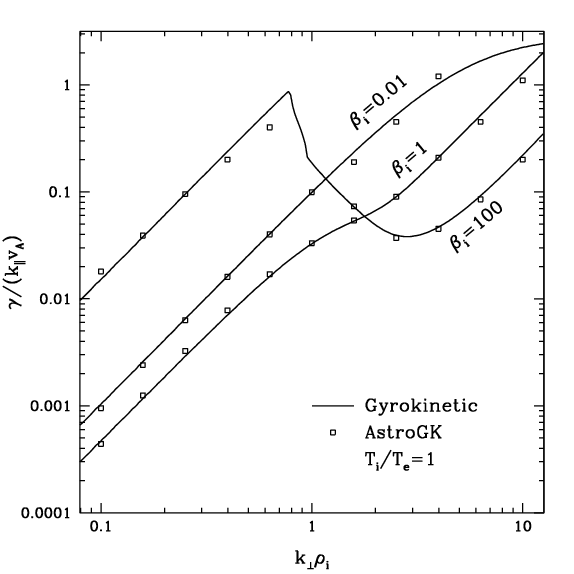
The model Laplace-Fourier transform solution given by \eqref{eq:lfmod} can be used to determine the frequencies and damping rates of linear modes on the \Alfven branch---including the kinetic \Alfven wave at $k_\perp \rho_i \gg 1$---over a wide range of plasma parameters. In Figures~\ref{fig:w_b1.ps}--\ref{fig:g_t1.ps} we present frequencies and damping rates for parameter choices $\beta_i = 0.01, 1 100$, $T_i/T_e=0.01,1,100$, and $k_\perp \rho_i \in [0.1,10]$.
|

|
|
|
Linear Ion to Electron Heating Ratios
Using the heating equations for gyrokinetics \cite{Howes:2006}, we calculate the ion to electron heating ratio $P_i/P_e$ from the linear collisionless gyrokinetic dispersion relation and compare it to the results of AstroGK. The results are presented in \figref{fig:pipe} for parameters $\beta_i=10$ and $T_{i}/T_{e}=100$, chosen to give a heating ratio that varies by many orders of magnitude around $k_\perp \rho_i \sim 1$. Parameters for these runs are \T{ntheta}$=64$, \T{ngauss}$=32$, \T{negrid}$=32$, and $\Delta t=0.1$. The results of \T{AstroGK} shows excellent agreement with theory over 7 orders of magnitude in $P_i/P_e$.

|